Ответы
Ответ дал:
0
Ответ:
Объяснение:
!!!!!!!!!!!!!!!!!!!!!!
Приложения:
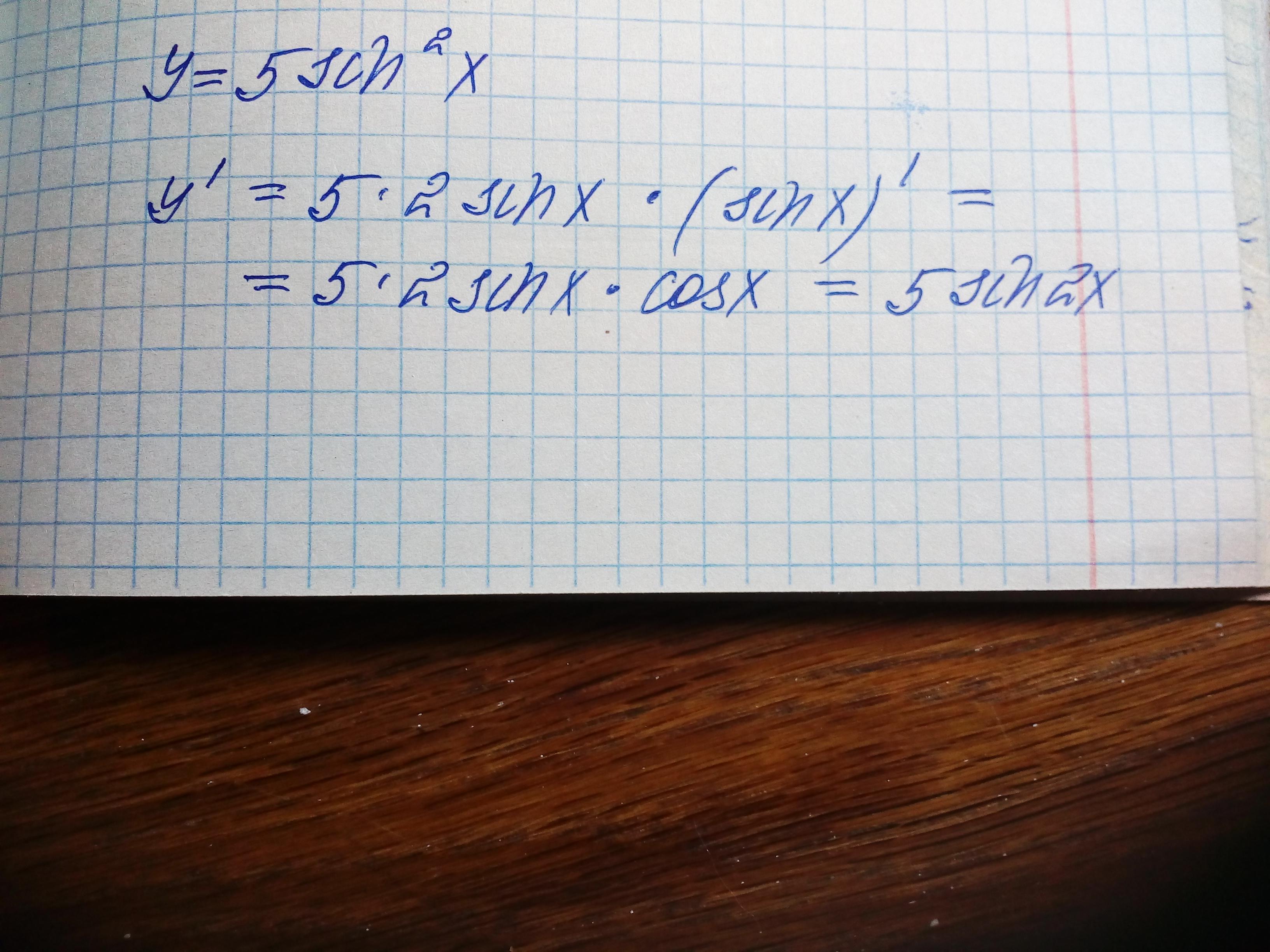
Ответ дал:
0
Найти производную сложной функции y =5sin²x
Ответ: 5sin2x
Объяснение: y =5sin²x u =sinx y =5u²
y'ₓ = y'u *u'ₓ = 5*2u*(sinx) '=10u*cosx= 10sinx*cosx = 5sin2x
- - - - - - - или ( усложняем )
y =5sin²x = 5(1 -cos2x) /2 = 5/2 - (5/2) cos2x
y ' = (5/2 - (5/2)cos2x) = (5/2) ' - (5/2)*(cos2x) ' = - (5/2)*(cos2x) '
нужно найти (cos2x) '
y₁ =cosu u =2x y₁'ₓ = y'u *u'ₓ = (-sinu)*(2x)ₓ' = - 2sinu = -2sin2x
y ' = (-5/2)*(-2sin2x) = 5sin2x
Приложения:
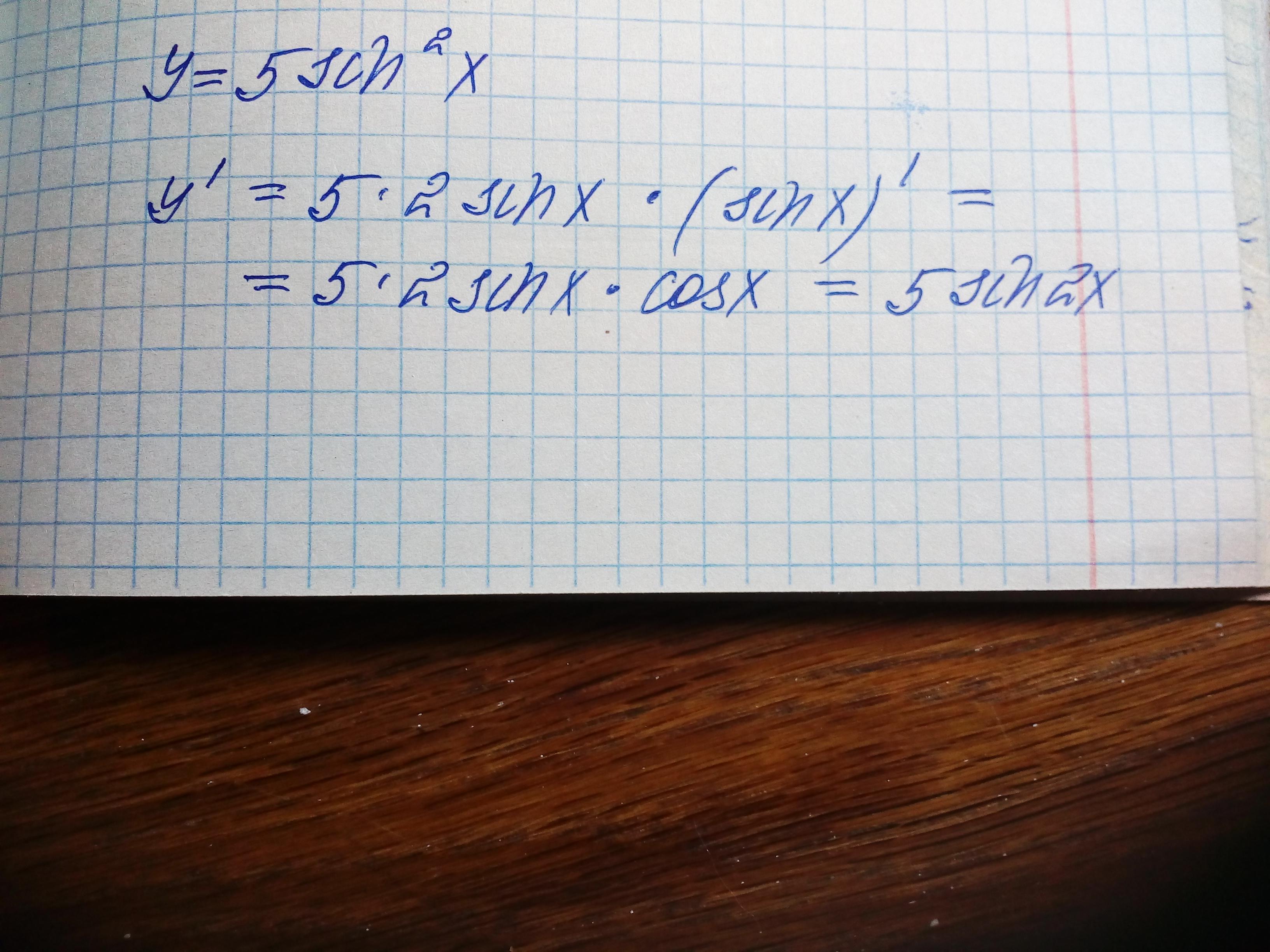
Вас заинтересует
2 года назад
3 года назад
3 года назад
8 лет назад
8 лет назад
9 лет назад