Question

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна 6,5 см, а один из катетов равен 12 см. Найти второй катет. ​

Answer 1

5 см

Объяснение:

по теореме Пифагора сумма катетов в квадрате равно гипотенузе в квадрате. медиана равна половине гипотенузы, поэтому гипотенуза равна 13 см. Из теоремы Пифагора следует что 169(13 в квадрате)-144(12 в квадрате)=25(5 в квадрате)

Answer 2

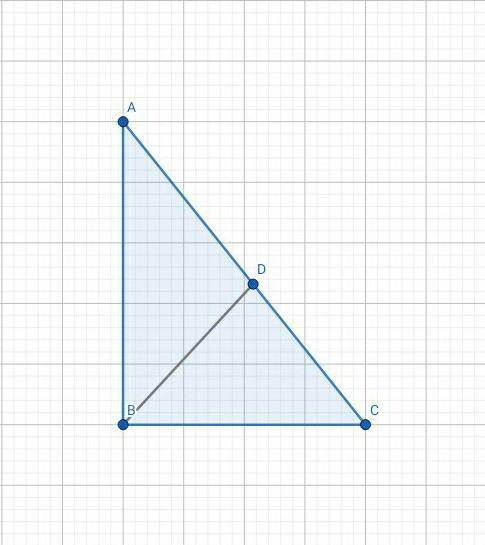
Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы (по свойству).

1. В прямоугольном△ABC:

AC = BD ⋅ 2 = 6,5 ⋅ 2 = 13 (см).

2. По теореме Пифагора:

AB = √(13² - 12²)

AB = √((13 - 12) ⋅ (13 + 12))

AB = √(1 ⋅ 25)

AB = √25 = 5 (см).

Ответ: AB = 5 (см).