Question

Помогите пожалуйста с геометрией
Вычислите площадь равнобедренной трапеции, основания которой равны 10 см и 26 см, если известно, что центр окружности, описанной около трапеции, находится на большем основании.
Ответ:___см^2​

Answer 1

Ответ:

36√65 см²

Объяснение:

Если вокруг трапеции можно описать окружность, то сумма оснований трапеции равна сумме боковых сторон.

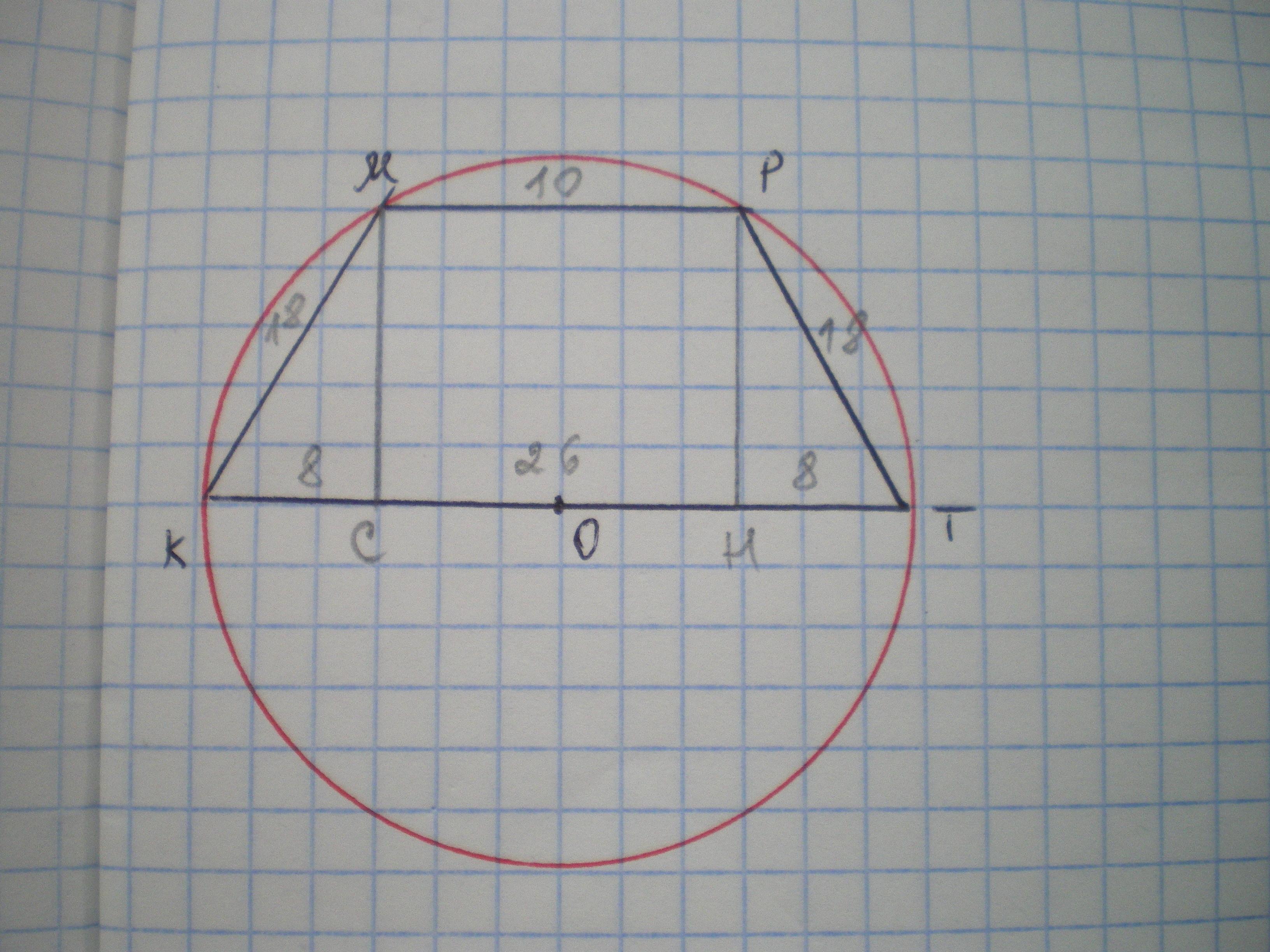
Пусть дана трапеция КМРТ, МР=10 см, КТ=26 см. КМ=РТ. Найти S(КМРТ).

МР+КТ=КМ+РТ=10+26=36 см

КМ=РТ=36:2=18 см

Проведем высоты МС и РН. ΔКМС=ΔТРН по катету и гипотенузе, значит, КС=ТН=(26-10):2=8 см.

Найдем РН по теореме Пифагора:

РН=√(РТ²-РН²)=√(324-64)=√260=2√65 см

S=(МР+КТ)/2*РН=(10+26)/2*2√65=36√65 см²