даю 60 баллов найдите число целочисленных решений неравенства
нужно сроооочно пжпжп
заранье спасибо
Приложения:
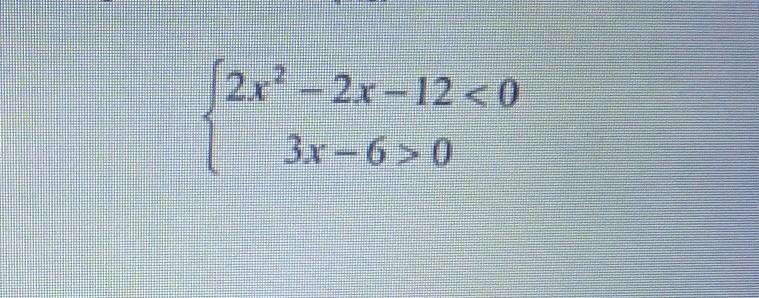
Ответы
Ответ дал:
0
По тереме Виета корнями уравнения будут числа -2 и 3, значит:
Так как 2>0 и 3>0, то система неравенств упрощается:
1)
+ - +
__________-2___________3__________________
Решение первого неравенства: -2 < x < 3
2)
это решение второго неравенства
3) Общее решение: -2 < x < 2
Перечислим целочисленные решения из этого промежутка:
-1; 0; 1
Всего три!
Ответ: 3
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
8 лет назад
9 лет назад