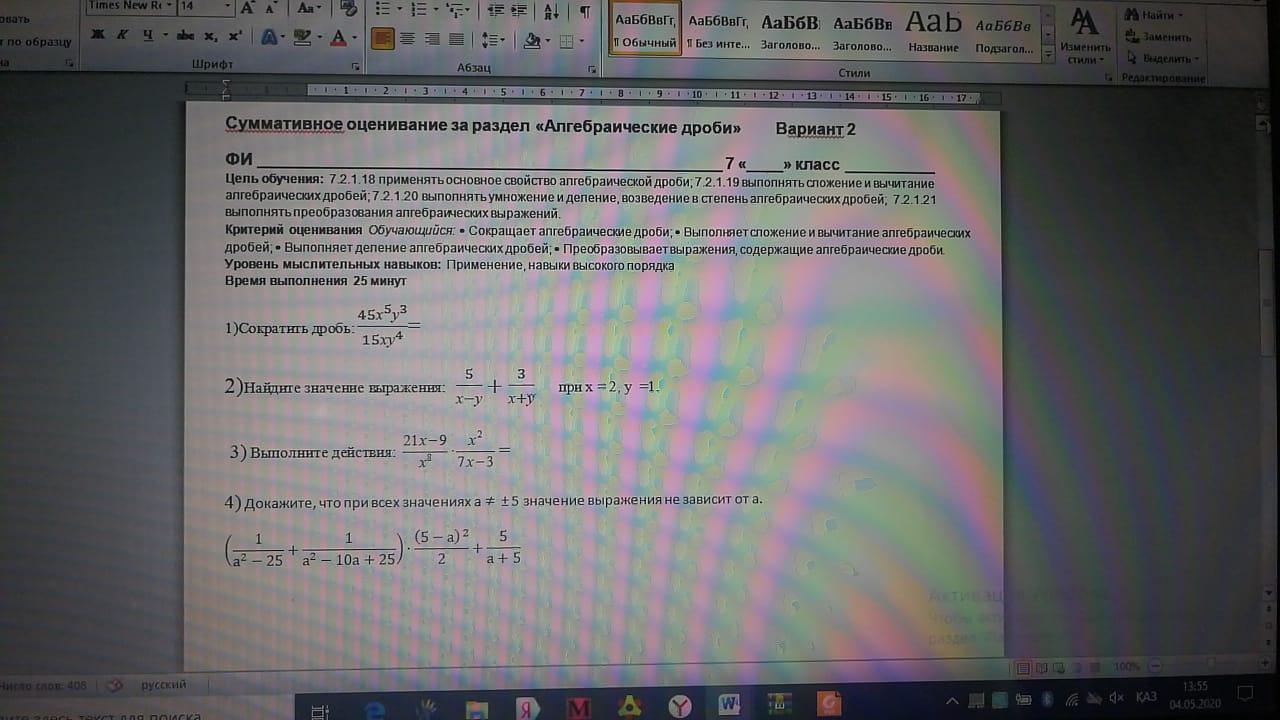
Ответы
Ответ дал:
0
Ответ:
№1 -
№2 - 6
№3 -
Объяснение:
№1
=
(разность степеней с одинаковыми основаниями)
№2
5+ 1 = 6
(дроби при подстановке значений - сокращаются)
№3
*
=
(значения сокращаются, в 21x - 9 это тоже самое как 3(7x - 3), а со степенями я уже сказал выше)
№4
*
+
=
*
+
=
*
+
=
+
=
=
(ля пример неприятный, но попытался( )
Ответ дал:
0
Объяснение:
№1
№2
При x = 2 y = 1
№3
№4
1) Решим сначала то, что в ( )
2) Проведём действие с *
3)
Из этого можно сделать вывод, что при любом значении А данное выражение равно 1, то есть выражение не зависит от А.
Вас заинтересует
2 года назад
9 лет назад
9 лет назад
10 лет назад