Виділіть з квадратного тричлена квадрат двочлена та доведіть, що при будь-якому значенн в х квадратний тричлен набуває від'ємного значення
Приложения:
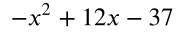
Ответы
Ответ дал:
0
Ответ: максимального значення вираз досягая при умові , а саме
, при будь-якому відмінному від 6 значенні x вираз набуватиме ще менших значень
Объяснение:
Вас заинтересует
3 года назад
3 года назад
9 лет назад
10 лет назад