Question

В окружности с радиусом 6см проведена хорда длиной 6см. Чему равна длина дуги стягиваемая ею? Найти площадь полученного сектора.

Answer 1

Ответ:   $l_1=2pi ; ; ,; ; l_2=10pi ; ; ,; ; S=3cdot (2pi -3sqrt3); .$

Объяснение:

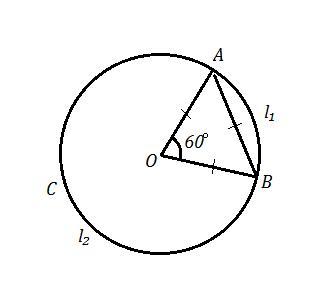
Так как длина хорды АВ = радиусу окружности R=OA=OB, то ΔAOB - равносторонний и все его углы = 60° .

Значит центральный угол АОВ=60°. Тогда длина дуги АВ равна

$l_1=dfrac{pi Rcdot alpha }{180^circ }=dfrac{pi cdot 6cdot 60^circ }{180^circ }=dfrac{6pi }{3}=2pi$

Длина второй дуги окружности ACB равна

$l_2=dfrac{pi cdot Rcdot (360^circ -60^circ )}{180^circ }=dfrac{pi cdot 6cdot 300^circ }{180^circ }=10pi$  

Площадь сегмента, соответствующего углу в 60° равна:

$S=dfrac{R^2}{2}Big (dfrac{pi alpha}{180^circ }-sinalpha Big)=dfrac{36}{2}Big(dfrac{pi cdot 60^circ }{180^circ}-dfrac{sqrt3}{2}Big)=18cdot Big(dfrac{pi}{3}-dfrac{sqrt3}{2}Big)=\\=3cdot (2pi -3sqrt3)$