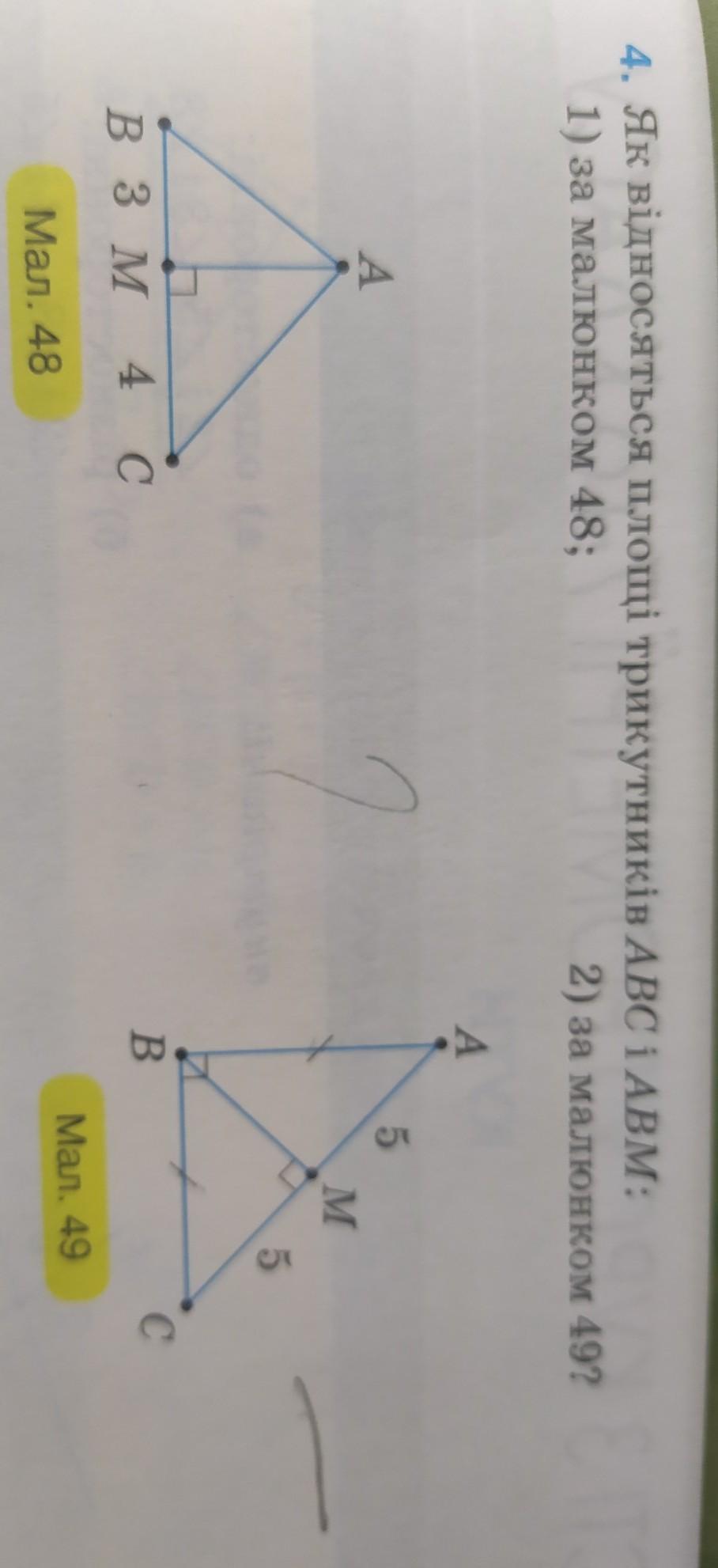
Ответы
1) У треугольников АВС и АВМ одинаковая высота - АМ. Их площади будут относиться как основания (основанием будет считать сторону, к которой проведена высота АМ).
Основание треугольника АВС - ВС (ВМ+МС = 3+4 = 7).
Основание треугольника АВМ - ВМ (3).
Тоесть,
2) Рассмотрим отрезок ВМ - медиана (так как делит противоположную сторону на равные отрезки). Но также это и высота, а значит, треугольник АВС не только прямоугольный, но и равнобедренный.
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине. Тоесть, ВМ = 5.
Площадь треугольника АВС равна половине произведения высоту на сторону, к которой проведена эта высота.
В данном случае -
Но также мы знаем, что медиана делит треугольник на два равновеликих треугольника. Тоесть, площадь треугольника АВМ в два раза меньше площади треугольника АВС.