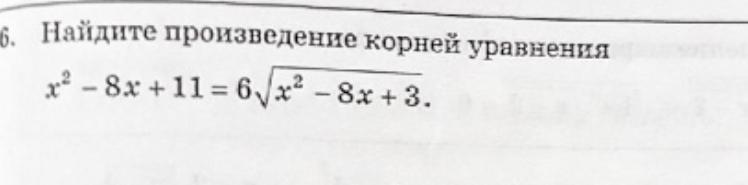Question

РЕШИТЕ УРАВНЕНИЕ. ДАМ 10 БАЛЛОВ

Answer 1

Ответ: 13

Пошаговое объяснение:

1) Сначала найдём область допустимых значений x

$x^{2} - 8x + 3 geq 0$

$D = b^{2} - 4ac = 64 - 12 = 52$

$x_{0} =frac{8+-sqrt{52} }{4} = 4 +- sqrt{13}$

х ∈ (-∞; 4 - √13] U [4 + √13; +∞)

2) Пусть $sqrt{x^{2} - 8x + 3} = t$, тогда $x^{2} - 8 x + 3 = t^{2}$

Составляем уравнение и находим корни:

$t^{2} + 8 = 6t$

$t^{2} -6t+8=0$

t = 4; t = 2.

t² = 16; t² = 4

3) Находим х

$left {{{x^{2} -8x +3 = 4} atop {x^{2} - 8x +3 = 16}} right.$

$left { {{x^{2} - 8x - 1=0} atop {x^{2} - 8x - 13 =0}} right.$

$left { {{D_{1} =64+4*1 = 68} atop {D_{2} =64 + 14*4 = 116}} right.$

$left { {{left { {{x_{1} =frac{8+sqrt{68} }{2} = 4 + sqrt{17} } atop {x_{1} =frac{8-sqrt{68} }{2} }=4-sqrt{17} } right. } atop {left { {{x_{3} =frac{8+sqrt{116} }{2} = 4+sqrt{29} } atop {x_{4} =frac{8 - sqrt{116} }{2} = 4 - sqrt{29} }} right. }} right.$

Все корни принадлежат области допустимых значений.

Находим произведение корней уравнения:

(4 - √17)(4 + √17)(4 - √29)(4 + √29) = (16 - 17) (16-29) = (-1) * (-13) = 13

Ответ: 13