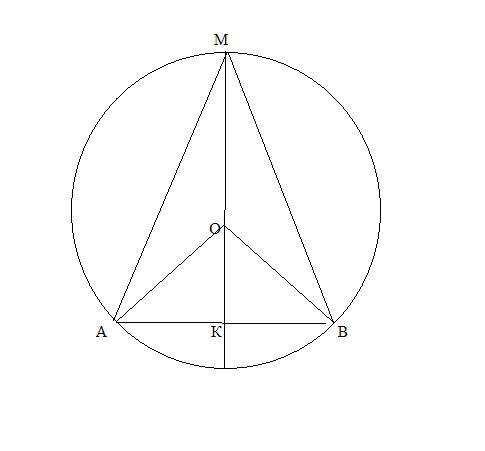
Два конуса (один внутри другого) построены на одном основании. Углы между образующими и высотой конуса равны 300 и 600 . Разность высот равна
12√3. Площадь сферы, описанной около большого конуса, равна πk, найдите k.
Ответы
Два конуса (один внутри другого) построены на одном основании. Углы между образующими и высотой конуса равны 300 и 600 . Разность высот равна
12√3. Площадь сферы, описанной около большого конуса, равна πk, найдите k.
Объяснение:
Рассмотрим сечение данной комбинации тел , проходящее через высоты конусов. Центр О ,описанной окружности около большего ΔАВМ, лежит на серединном перпендикуляре, который совпадает с высотой МК, т.к. МА=МВ образующие конуса.
Вершина О малого конуса лежит на высоте большого конуса .
ΔОАВ-равнобедренный,т.к. ОА=ОВ образующие малого конуса ⇒ОА=ОВ=R и ОА=ОВ=ОМ=R.
По условию задачи S(сферы )=πк , ∠АМК=30°,∠АОК=60°, H-h=12√3 , H-высота большого конуса , h-высота малого конуса
Т.к. H-h=12√3 , то МО= 12√3 ⇒ R =12√3.
S(сферы )=4πR² и S(сферы )=πк приравняем правые части:
4π(12√3)²=πк
к =4*144*3, к=12³ или к=1728