Найти общее решение или общий интеграл дифференциального уравнения. Решить задачу Коши.
если не составит труда, то можно с пояснением, большое спасибо
Приложения:
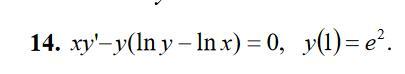
Ответы
Ответ дал:
0
Пусть
Сделаем проверку:
Таким образом, — имеем однородную функцию нулевого измерения.
Сделаем замену: , где
. Тогда
Имеем:
Рассчитаем интегралы:
Обратная замена:
— общее решение
Из начальных условий имеем:
Частное решение:
Ответ:
Вас заинтересует
2 года назад
2 года назад
3 года назад
8 лет назад
9 лет назад