Question

Помогите пожалуйста!!


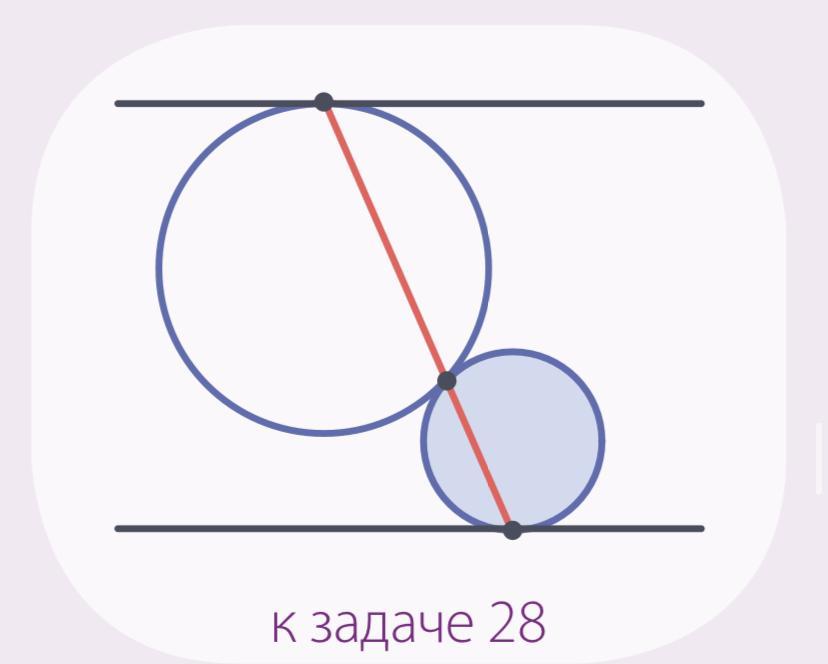
Две окружности касаются внешним обра­ зом, причем каждая из них касается одной из двух параллельных прямых так, как это показано на рисунке. Докажите, что три получившиеся точки касания лежат на одной прямой.

Answer 1

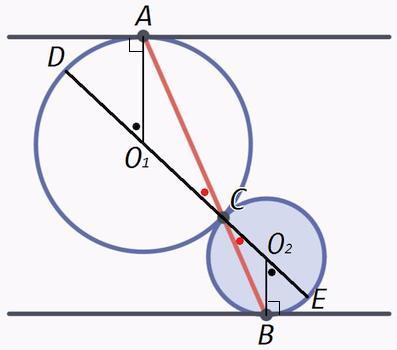
Проведем линию центров.

Точка касания двух окружностей (C) лежит на линии центров (DE).

Радиусы O1A и O2B перпендикулярны параллельным, следовательно параллельны.

AO1D=BO2E (внешние накрест лежащие) => ∪AD=∪BE => ACD=BCE

ACD и BCE -  вертикальные углы (равные углы отложены по разные стороны от прямой DE)

Лучи CA и CB составляют прямую.