Question

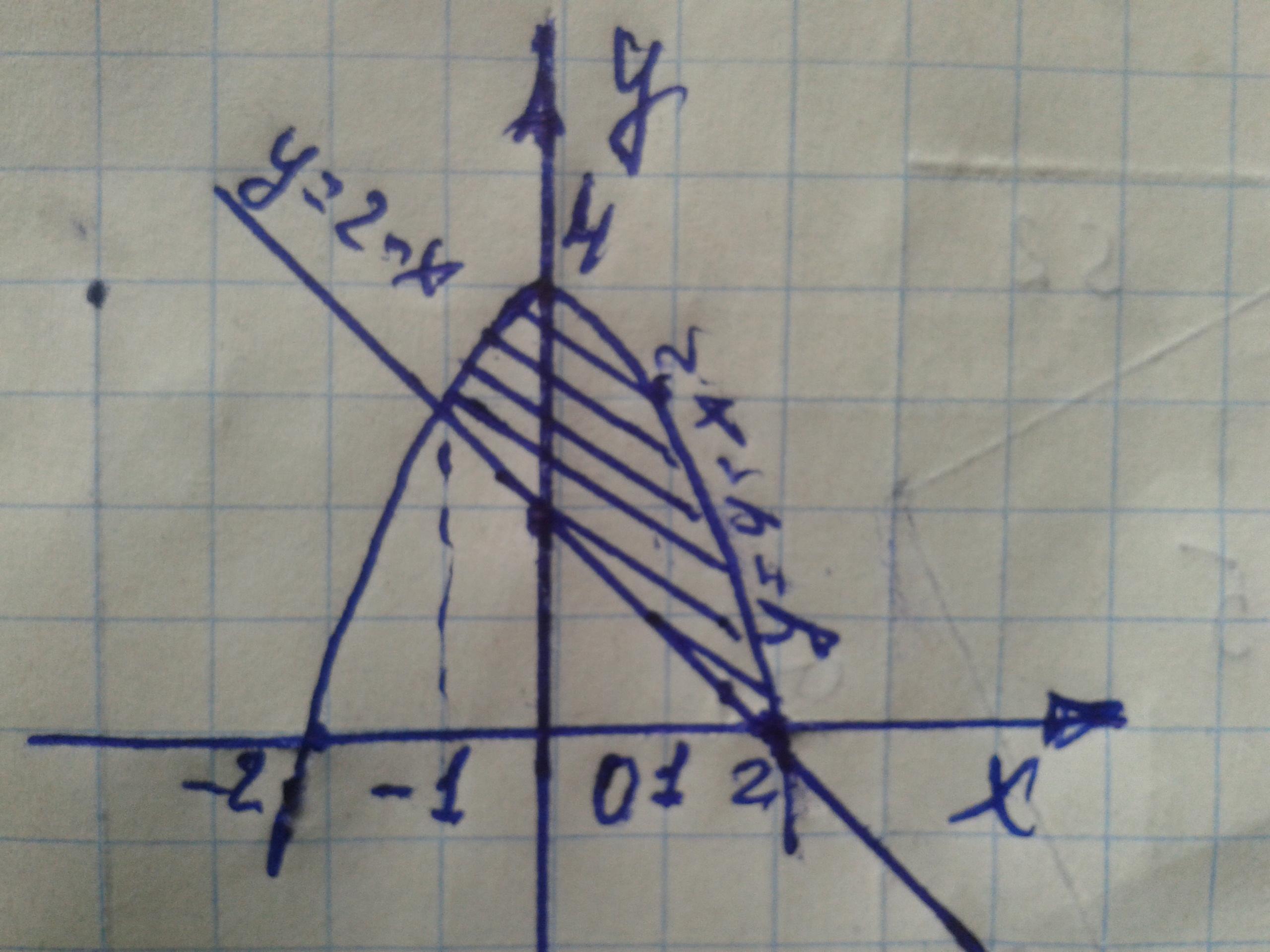
Обчислити площу фігури обмеженої параболою у= 4 - х^2 і прямою у=2-х
Это срочно! Если можно. С рисунком

Answer 1

Ответ: S=4,5 кв. ед.

Объяснение:

y=4-x²     y=2-x      S=?

4-x²=2-x

x²-x-2=0     D=9      √D=3

x₁=-1      x₂=2

$intlimits^2_{-1} ({4-x^{2}-2+x) } , dx =intlimits^2_{-1} {(2+x-x^{2} } ), dx =(2x+frac{x^{2} }{2} -frac{x^{3} }{3} )|_{-1}^{2} } =\=2*2+frac{2^{2} }{2} -frac{2^{3}}{3} -(2*(-1)+frac{(-1)^{2} }{2} -frac{(-1)^{3} }{3} )=4+2-frac{8}{3} -(-2+frac{1}{2}-frac{(-1)^{3} }{3} )=\ =6-frac{8}{3} +1,5-frac{1}{3}=7,5-3=4,5.$