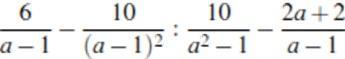Ответы
Ответ дал:
0
Ответ:
В РЕШЕНИИ!!!!
Объяснение: Запишем выражение в исходном виде:
Преобразуем выражение:
Тут обе дроби нужно преобразовывать, а потом их делить!!!!
На это уходит много времени
мерзотно
ЧЕРЕСЧУР ГРОМОЗДКО, И ДОЛГО РЕШАТЬ
НУЖНО ЕЩЕ И ПРОВЕРЯТЬ ВСЕ ВЫКЛАДКИ
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад