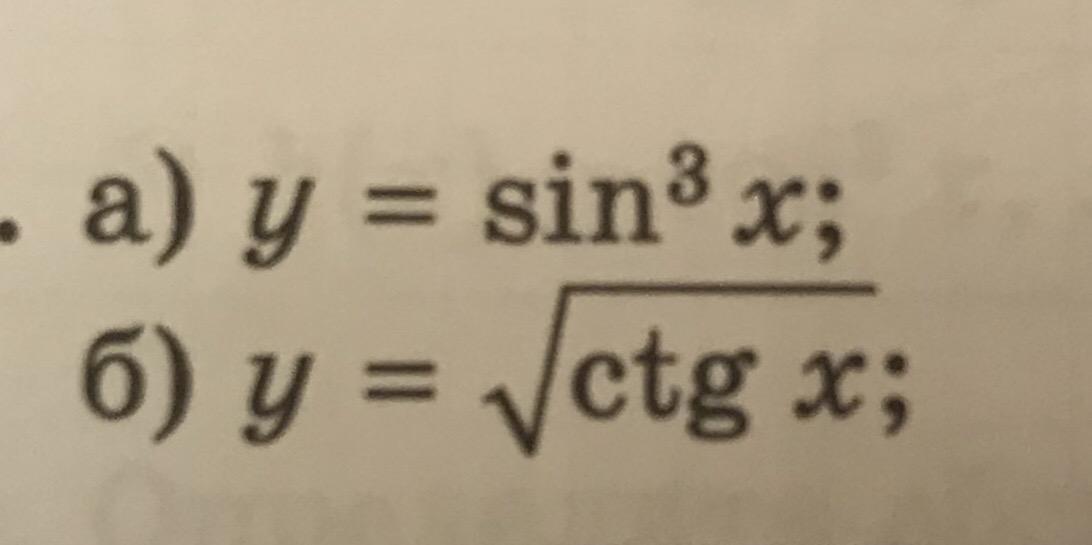Ответы
Ответ дал:
0
Ответ дал:
0
а)Находим, как произведение производной от степенной на тригонометрическую. по формуле ( uⁿ)'=n*uⁿ⁻¹*u'; u=sinx;
y'=3(sin²x)*cosx;
б) Здесь берем производную от корня, а потом от подкоренного выражения и умножаем. (√u)'=1/2√u)*u' в качестве u=ctgx;
y'=(√ctgx)'=(1/(2√ctgx))*(-1/sin²x)=-1/(2√ctgx*sin²x)
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад