Question

Помогите пожалуйста 11!!!!!

Answer 1

Ответ:3)2

Пошаговое объяснение:

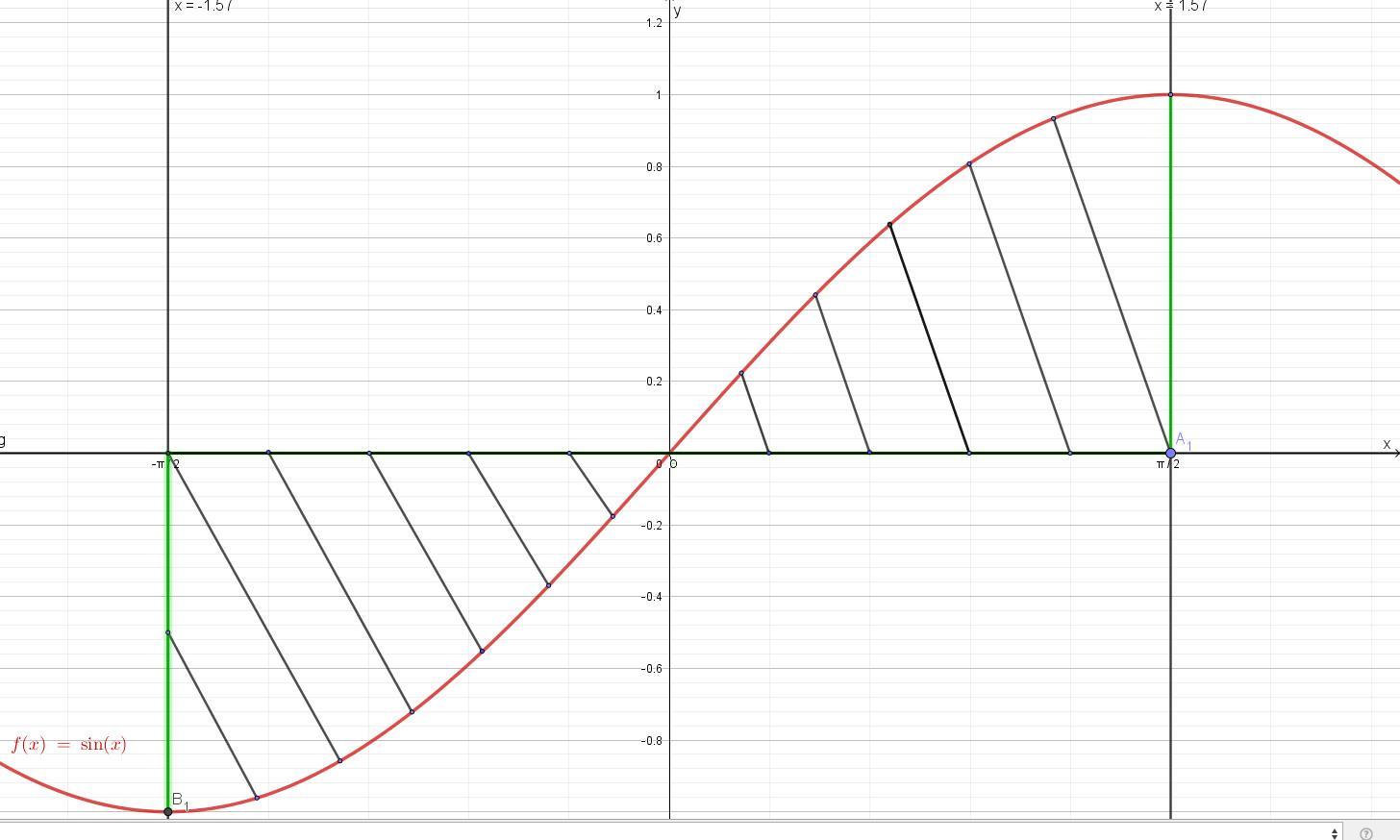
Найдите площадь фигуры ограниченной линиями у =sin(x), y = 0, x = -π/2, x = π/2.

Начертим все линии(смотри рисунок во вложении).

Получим в интервале от -π/2 до 0  фигуру ограниченную сверху прямой у=0,  снизу синусоидой у = sin(x), а в интервале от 0 до π/2 еще одну фигуру  ограниченную сверху синусоидой у = sin(x), снизу прямой у =0.

Поэтому площадь фигуры будет состоять из суммы  двух определенных интегралов

$S =intlimits^0_{-pi/2} {(0-sin(x))} , dx +intlimits^{pi/2}_0{(sin(x)-0)} , dx= -intlimits^0_{-pi/2} {sin(x)} , dx +intlimits^{pi/2}_0{sin(x)} , dx=$

$=cosxbegin{vmatrix}0\-pi/2end{vmatrix}-cosxbegin{vmatrix}pi/2\0end{vmatrix}=cos(0)-cos(-pi/2)-cos(pi/2)+cos(0)=1+1=2$