Question

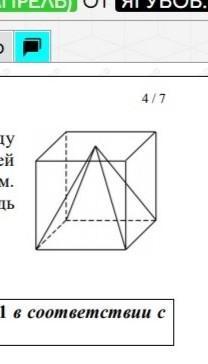
3.В куб вписали правильную
четырёхугольную пирамиду таким
образом, что её основание совпадает с
одной из граней куба, а её вершина
касается противоположной стороны (см.
рисунок). Найдите объём куба, если
известно, что площадь боковой
поверхности пирамиды равна 4 корня из 5​

Answer 1

Пусть сторона куба равна а.

Проведём осевое сечение пирамиды перпендикулярно ребру основания. Получим равнобедренный треугольник.

Высота его по условию равна а.

Боковая сторона - это апофема А пирамиды.

А = √(а² + (а/2)²) = а√5/2.

Боковая поверхность Sбок = (1/2)РА = (1/2)*4а*(а√5/2) = а²√5.

Приравняем заданному значению:

а²√5 = 4√5.

Отсюда а = √4 = 2.

Ответ:  V(куба) = а³ = 2³ = 8 куб.ед.