Question

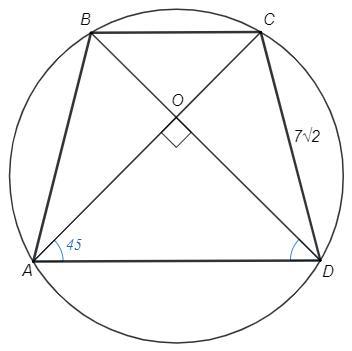
Диагонали равнобедренной трапеции перпендикулярные. Найдите радиус окружности, описанной около трапеции, если её боковая сторона равна 7√2 см.

Плагиат БАНИТСЯ ! Неполные ответы отправятся на ДОРАБОТКУ ! Леди и джентельмены, убедительно прошу выполнить решение максимально ПОДРОБНО и ПОНЯТНО (разборчиво, если от руки) и, что самое главное, объяснить, НА КАКИХ ОСНОВАНИЯХ ТРАПЕЦИЯ ДОЛЖНА ПРЕВРАТИТЬСЯ В КВАДРАТ, т. е. почему основания трапеции должны стать равными (если это действительно так), как заявляют в своих решениях некоторые "специалисты". Первый, кто успешно решит задачу и выполнит мою просьбу, получит 50 + дополнительные 25 баллов! Успехов, друзья! Целую, обнимаю!

Answer 1

Равнобедренная трапеция, углы при основании равны.

BA=CD, BAD=CDA

△BAD=△CDA (по двум сторонам и углу между ними)

BDA=CAD, △AOD - равнобедренный прямоугольный.

CAD =90/2 =45

sin(CAD) =1/√2

Теорема синусов

CD/sin(CAD) =2R => R =7√2 *√2 /2 =7 (см)

Answer 2

Ответ:

Объяснение:решение смотрите во вложении