Question

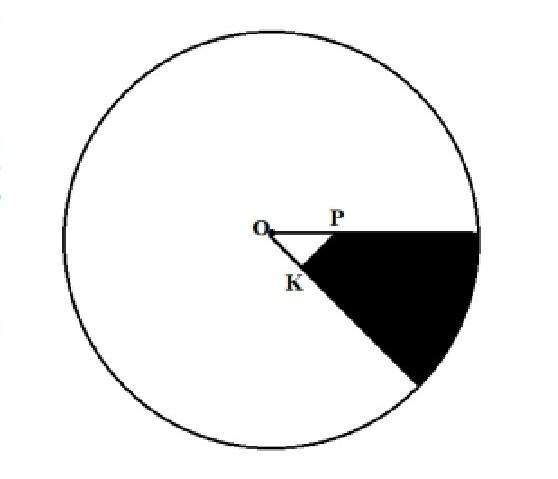
на рисунке изображён сектор круга с центром в точке О и радиусом, равным 12 см. ОР=4 см РК перпендикулярен ОК и угол РОК равен 45 градусов найдите площадь закрашенной области​

Answer 1

Ответ:

Пошаговое объяснение:

Площадь сектора с радиусом R=12 см и углом а=45°

S(сек) = Π*R^2*a/360° = 3,14*12^2*45°/360° = 3,14*144/8 = 56,52 кв.см.

Треугольник OPK имеет углы 45°, 45° и 90° и гипотенузу OP = 4 см.

Его катеты OK = KP = 4/√2 = 2√2 см, а площадь

S(OPK) = OK*KP/2 = 2√2*2√2/2 = 4 кв.см.

Площадь закрашенной области

S = S(сек) - S(OPK) = 56,52 - 4 = 52,52 кв.см.