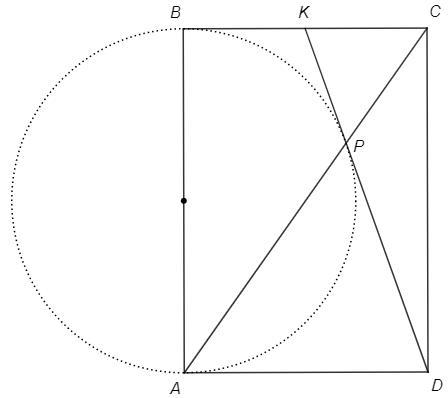
На стороне AB прямоугольника ABCD как на диаметре построена окружность ω. Пусть P — вторая точка пересечения отрезка AC и окружности ω. Касательная к ω в точке P пересекает отрезок BC в точке Kи проходит через точку D. Найдите AD, если известно, что KD=42
Сроооочнооо помогите,пожалуйста
Ответы
Ответ дал:
17
BC, AD - касательные (т.к. перпендикулярны диаметру)
BK=KP, AD=DP (отрезки касательных из одной точки)
△ADP - равнобедренный
△CKP~△ADP (по накрест лежащим при BC||AD)
△CKP - равнобедренный, CK=KP
KP=CK=BK =BC/2 =AD/2
KD =KP+DP =AD/2 +AD =3/2 AD
AD =2/3 KD =42*2/3 =28
Приложения:
mito3377:
почему СК=КР и почему треугольник СКР?
Треугольники ADP и CKP подобны. ADP равнобедренный, следовательно CKP тоже равнобедренный.
спасибо
А как вам такое? :) Очевидно (сравнением углов), что KO II CA ... или даже еще проще :) BP перпендикулярно AC => треугольник BPC прямоугольный => BK = KP = KC = AD/2 => AD = DP = (2/3)KD. Забавно :) на ютубе часто такие задачки выкладывают в качестве "вирусных". Чаще всего они очень простые, "одноходовки".
То, что KO II CA, сразу дает BK = KC; O - конечно, центр окружности.
Вот наиболее красивое и понятное решение этой простенькой задачки :) Точки касания B и P симметричны относительно KO. => Равны углы CAB и KOB; (оба равны половине центрального угла POB) => KO II CA; Дальше BO = AO => BK = KС= (тут уже все решено, дальше уже чистая схоластика) = KР = BC/2 = AD/2 => AD = DP = (2/3)KD; Вот. Это - то, что надо :)
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад