Ответы
Ответ дал:
1
1. Пусть
Решать надо методом интервалов, для этого надо найти нули функции , решим для уравнение
Получаем разложение
Там интервалы были, знаки на них +-+, выбрали средний
Возвращаемся к замене
Такой переход имели право сделать, так как функция - монотонно возрастающая функция.
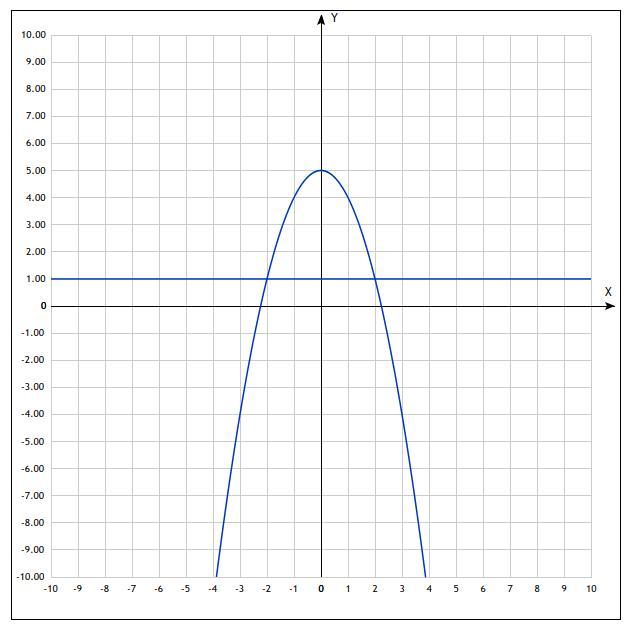
2. - парабола с ветвями, направленными вниз,
- просто прямая и фигура, образованная при их пересечении будет такова, что кусок параболы будет лежать выше.
Вспомним, что для на некотором интервале, то площадь фигуры будет равна
В нашем случае нужно вычислить пределы, а это как раз абсциссы точек пересечения, то есть нужно решить уравнение
, пределы нашли, вычисляем:
Приложения:
HODATI:
Спасибо! Проверил себя и увидел недочеты. Отдельная благодарность за объяснение :)
Вас заинтересует
1 год назад
1 год назад
3 года назад
8 лет назад