Question

Помогайте пацаны.


Чтобы сделать витраж в виде мозаики, стекольщик режет равнобедренную трапецию на два равнобедренных треугольника. Для этого он соединяет две несмежные вершины трапеции и исполняет задуманное. Найдите углы трапеции. Ответ дайте в градусах.

Answer 1

Ответ:

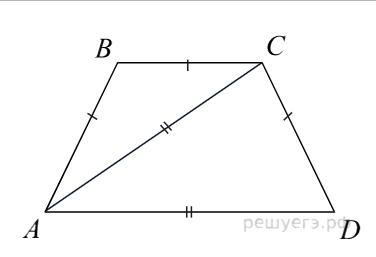
Если AB=BC то треугольник ABC — равнобедренный с основанием AC. Если AC=AD то треугольник ADC — равнобедренный с основанием CD. Так как углы при основании равнобедренного треугольника равны, то ∠BAC=∠BCA, ∠ADC=∠ACD. Далее ∠DAC=∠BCA как внутренние накрест лежащие при AD║BC и секущей AC.

Пусть ∠BAC=x, тогда ∠BAC=x, ∠DAC=x. Тогда ∠BAD=∠BAC+∠DAC=2x. Тогда ∠ADC=∠BAD=2x как углы при основании равнобедренной трапеции. Следовательно, ∠ACD=2x, ∠BCD=∠BCA+∠ACD=3x. По свойству равнобедренной трапеции имеем ∠BAD+∠BCD=180°. Составим уравнение:  2x+3x=180⇔x=36°

Значит,  ∠BAD=2×36=72°, ∠BCD=3×36=108°.

Ответ: 72° и 108°.

Объяснение: