Question

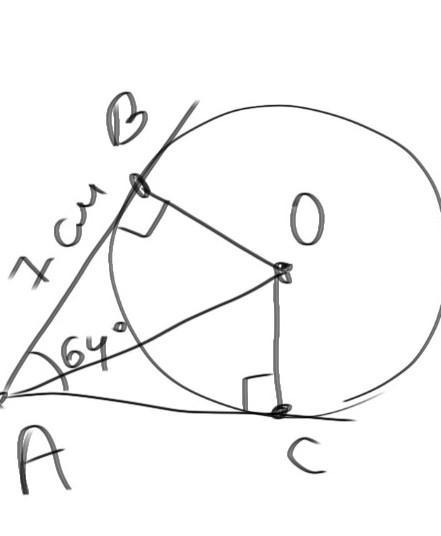
Из точки А к окружности проведены две касательные, точки В и С – точки касания. Угол ВАС равен 64 градуса, АВ=7 см. Найти АС и угол ВАО, где точка О – центр данной окружности.

Answer 1

Ответ:

АС=7 см

Угол ВАО=32 градуса

Объяснение:

Теорема. Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Касательные АВ и АС выходят из одной точки А.

Получаем: АВ=АС=7 см

Угол ВАО=угол ОАС=1/2 угла ВАС

Угол ВАО=64:2=32 градуса