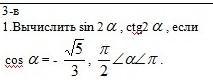Ответы
Ответ дал:
1
Вычислить sin2α , ctg2α ,если cosα = - √5 /3 , π/2 < α < π
Ответ: sin2α = -( 4√5 ) /9 ;
ctg2α = - (√5) /20 .
Объяснение: π/2 < α < π ( 2-ой четверт) sinα >0 ; sinα =√(1 -cos²α
sin2α =2sinα*cosα =2√(1 -cos²α)*cosα =2√(1 -( -√5 /3)²) *( - √5 /3) =
2√(1 - 5 /9) * ( - √5 /3) = 2√(4 /9) * ( - √5 /3) = 2*(2/3) * ( - √5 /3) = - 4√5 /9. - - - - - - - ctg2α =cos2α / sin2α
cos2α =cos²α - sin²α =cos²α - (1 -cos²α ) =2cos²α -1
cos2α =2(-√5/3)² -1 =10/9 -1 = 1/9
ctg2α =cos2α / sin2α =( 1/9 ) : ( -4√5) /9 = -1 /4√5 = - (√5) /20 .
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад