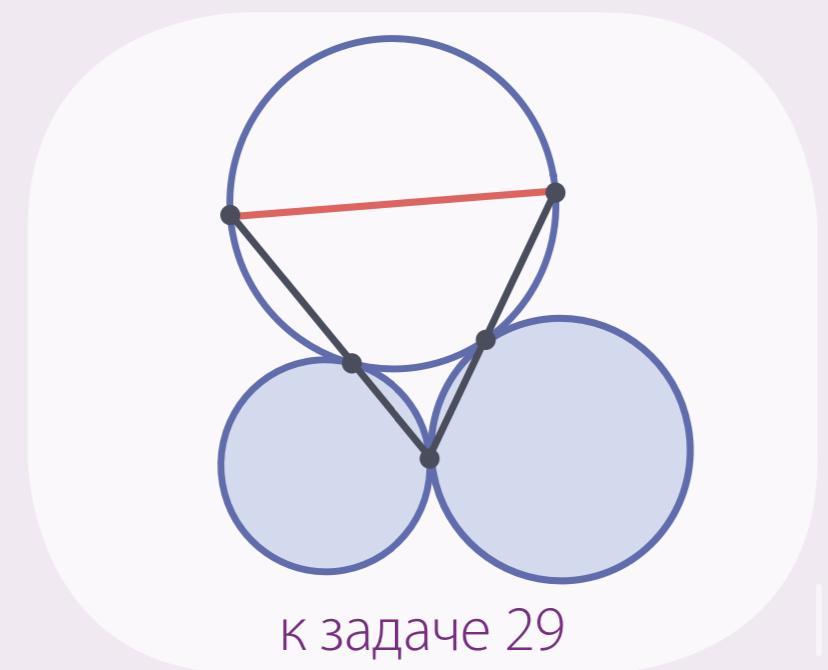
Три окружности касаются друг друга внеш ним образом. Две прямые, проходящие через точки их касания, вторично пере секают одну из этих окружностей в двух точках. Докажите, что эти две точки – диаметрально противоположны.
Приложения:
Ответы
Ответ дал:
3
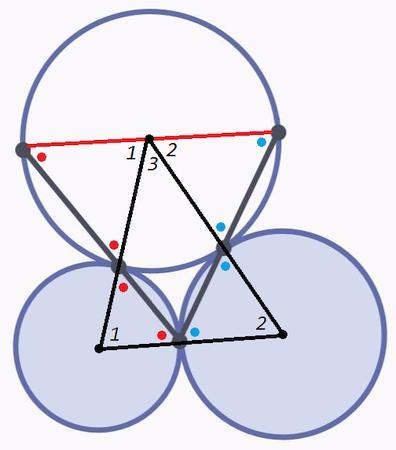
Соединим центры, точки касания лежат на линии центров.
Образованные радиусами равнобедренные треугольники подобны (углы при основании равны, вертикальные углы равны) - соответствующие углы равны.
1+2+3 =180 (сумма углов треугольника)
Красные радиусы составляют развернутый угол с вершиной в центре окружности, то есть диаметр.
Приложения:
std310705:
Можете пожалуйста решить еще одну задачу.)
https://znanija.com/task/37454316?answeringSource=feedPersonal%2FhomePage%2F1
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад