Question

Выберу ваш ответ ЛУЧШИМ! Помогите решить лишь 1 задание!
Известно, что площадь боковой поверхности правильной n-угольной пирамиды вдвое больше площади ее основания. Найти угол между боковой гранью и основанием пирамиды.

Відомо, що площа бічної поверхні правильної n-кутної піраміди вдвічі більша за площу її основи. Визначте кут між бічною гранню та основою піраміди.

Answer 1

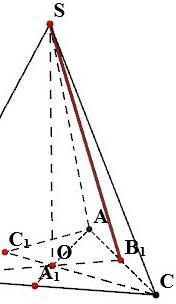
Пусть сторона основания AB = x, высота боковой грани SB1 = y, а высота пирамиды SO = h.

Площадь основания пирамиды S1=(√(3)/4) * x², площадь боковой грани S2= 0,5xy, площадь боковой поверхности S3 = 3 * S2=(3/2)xy.

По условиям задачи S3 = 2 * S1 -> (3/2)xy=2(√(3)/4) * x² -> y=x/√3

Косинус искомого угла a = OB1/SB1 = (0,5xtg(30g))/y = (0,5x(1/√(3))/(x * (1/√(3))), т.е. косинус равен 1/2, а это соответствует углу 60 градусов.

Ответ: 60 градусов.