Question

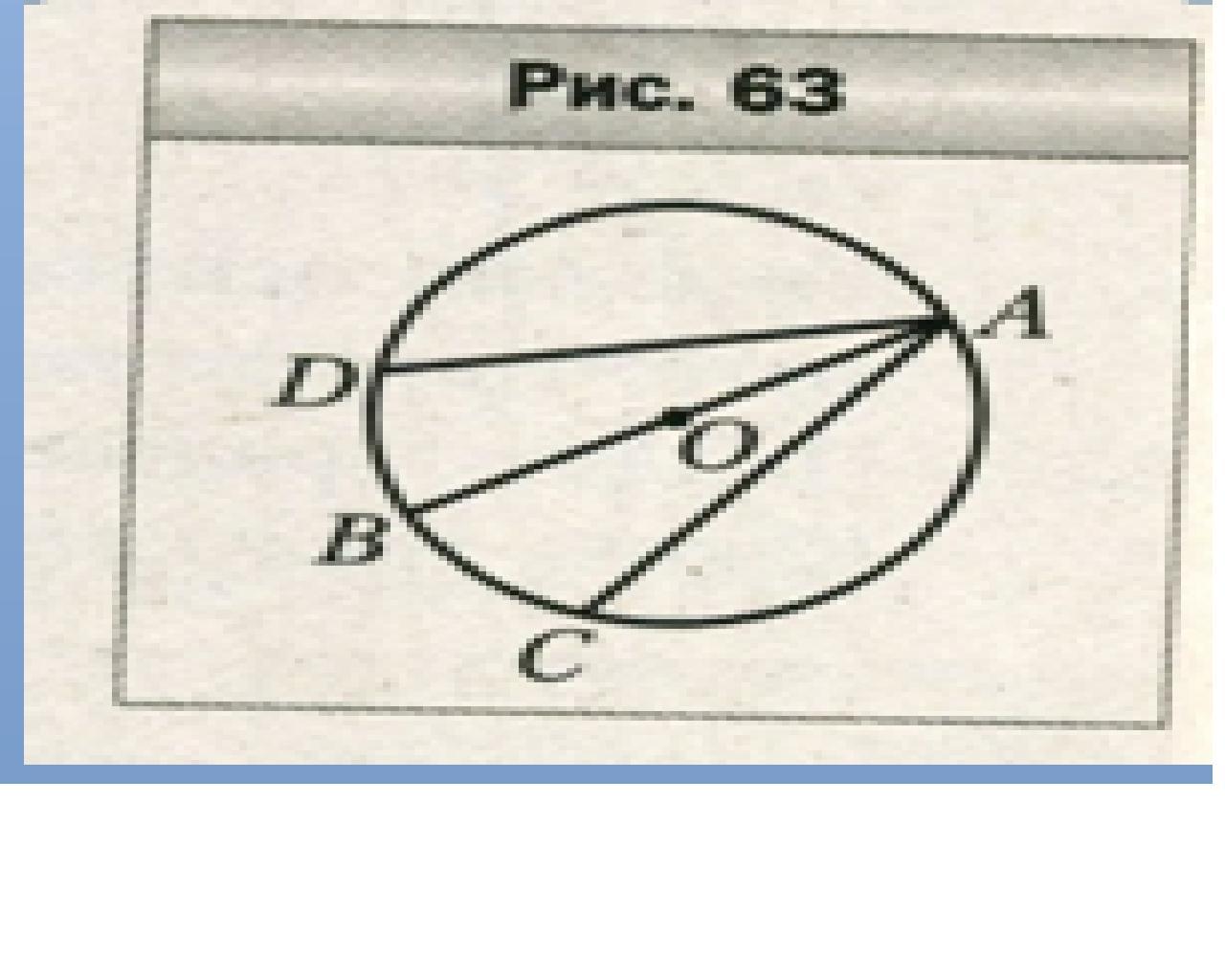
В окружности с центром O проведен ы диаметр AB и хорды AC и AD так, что ∠BAC = =∠BAD (рис. 63). Докажите, что AC = AD.

Answer 1

Ответ:

Соединим точки Д и С с центром окружности получим треугольники ДОА  и СОА - они равнобедренные (стороны радиуса окружности). В равнобедренном треугольники углы при основании равны, так как два угла одного равны двум углам другого (из условия) значит равны  и третьи углы. Треугольники равны - Если  две стороны и угол между ними одного треугольника равны двум сторонам и углу  между ними другого треугольника, то такие треугольники равны следовательно АД=АС.

Answer 2

В окружности с центром O проведен ы диаметр AB и хорды AC и AD так, что ∠BAC = =∠BAD (рис. 63). Докажите, что AC = AD.

Объяснение:

∠ВDA=∠BCA=90° как вписанные углы, опирающиеся на полуокружность в 180°.

ΔВDA=ΔBCA как прямоугольные по гипотенузе ( ВА-общая) и острому углу ( ∠BAC = =∠BAD по условию).

В равных треугольниках соответственные элементы равны⇒

AC = AD