1
Задание 18
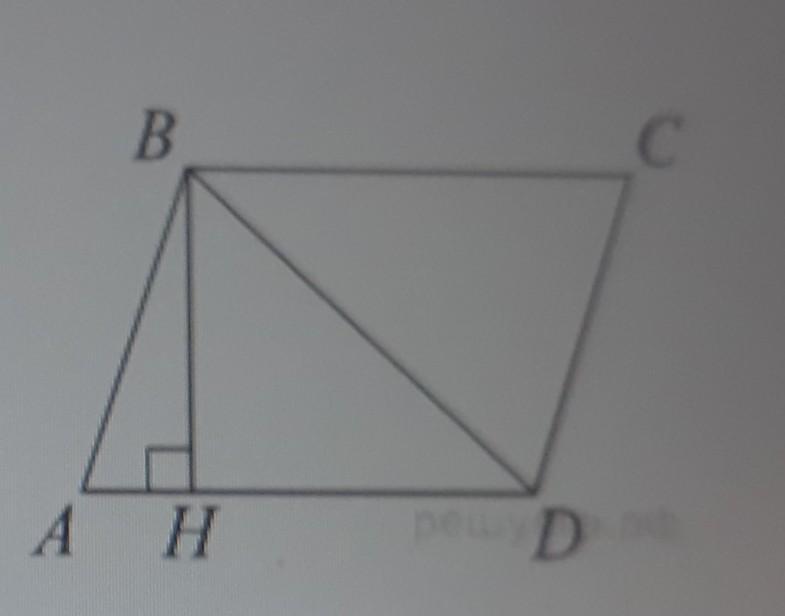
Высота ВН параллелограмма ABCD делит его сторону AD на отрезки АН = 4 и HD = 65.
Диагональ параллелограмма BD равна 97. Найдите площадь параллелограмма.
Приложения:
Ответы
Ответ дал:
7
Дано:
BH - высота
AH = 4; HD = 65
BD = 97
Найти:
S(ABCD) - ?
Решение:
Используем чертеж из условия!
Рассмотрим ΔBHD (∠H = 90°)
по теореме Пифагора:
BD² = BH² + HD²
97² = BH² + 65²
BH² = 97² - 65² = (97 - 65)(97 + 65) = 32 · 162 = 64 · 81 ⇒ BH = 8 · 9 = 72
AD = AH + HD = 4 + 65 = 69
S(ABCD) = AD · BH = 69 · 72 = 70 · 72 - 72 = 5040 - 72 = 4968
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад