Question

Гіпотенуза і катет прямокутного трикутника відносяться 5:3, а другий катет дорівнює 16 см. Знайдіть радіус кола, описаного навколо трикутника та площу трикутника.

Answer 1

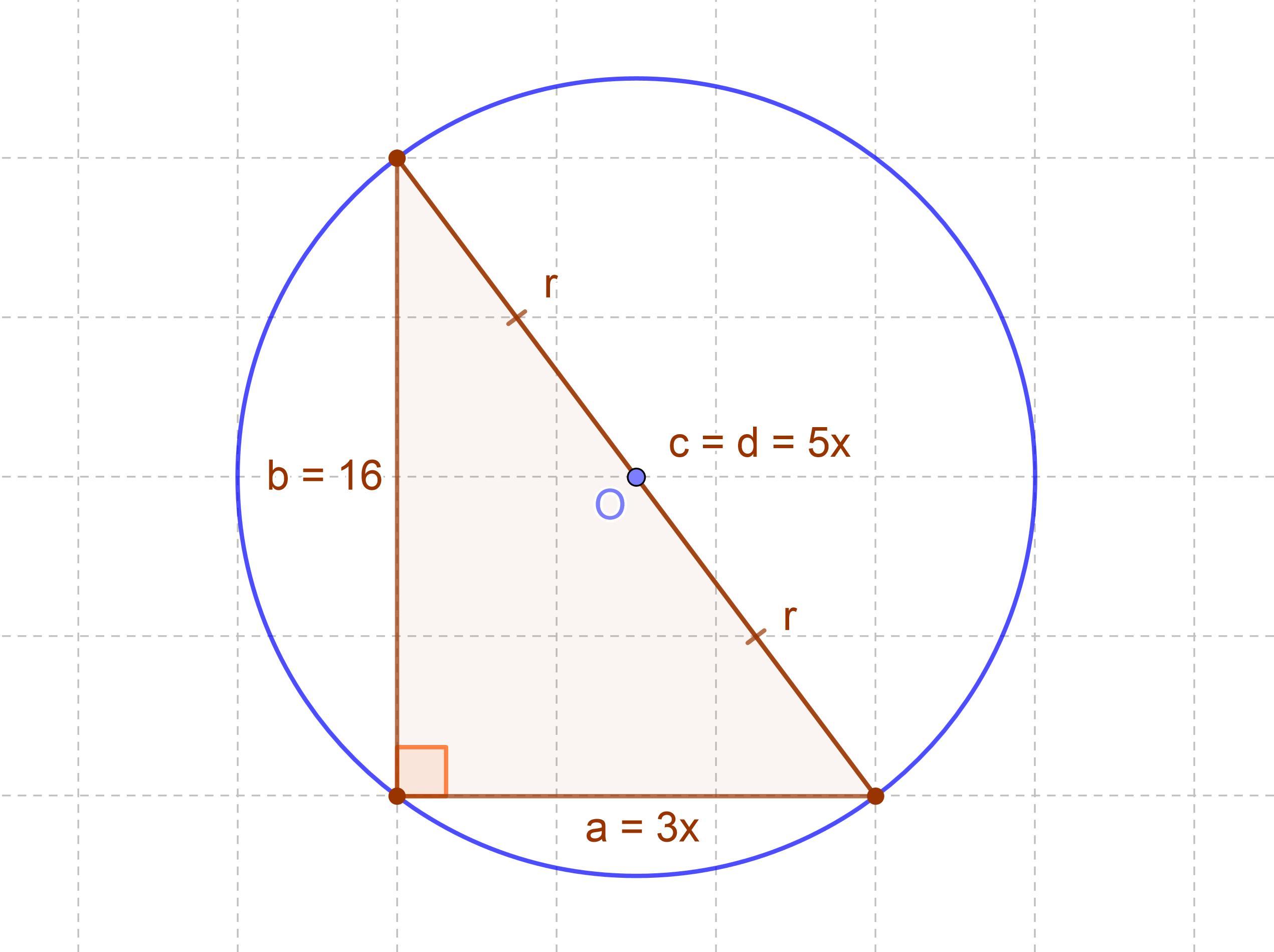
Дано: Δabc — прямокутний, де a, b — катети, c — гіпотенуза. c:a = 5:3, b = 16 cm.

Знайти: радіус описаного кола r, площу трикутника $S_{abc}$.

Рішення:

Нехай невідомий катет b = 3x cm, гіпотенуза c = 5x cm, а відомий катет a = 16 cm. Складемо математичну модель відповідно до т. Піфагора і вирішимо її:

    $a^2+b^2=c^2\:\: \Leftrightarrow \:\: (3x)^2+16^2=(5x)^2\\9x^2+16^2=25x^2\\16x^2=16^2\\x^2=\frac{\:\:16^2}{16} =16\\x=\pm \sqrt{16}= \pm 4$

Від'ємний корів відкидаємо, т.я. довжина не може бути від'ємною.

Тоді:

• невідомий катет b = 3x = 3·4 = 12 cm
• гіпотенуза c = 5x = 5·4 = 20 cm

Підставимо значення у формулу площі прямокутного трикутника:

    $S = \frac{a\cdot b}{2} = \frac{12\cdot 16}{2} = 12\cdot 8 = 96 \:\: (cm^2)$

Гіпотенуза прямого трикутника рівна діаметру описаного кола:

    c = d = 20 cm

Радіус кола рівний половині діаметра:

    r = d/2 = 20/2 = 10 cm

Відповідь: r = 10 cm, S = 96 cm².