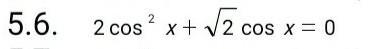Ответы
Ответ дал:
0
2cos (x)^2 + √2cos (x) = 0
1. Вынести за скобки общий множитель:
cos (x)(2cos (x) + √2) = 0
cos (x) = 0; 2cos (x) + √2 = 0.
2. Ищем x’ы:
cos (x) = 0
x = π/2 + kπ (k ∈ Z)
2cos (x) + √2 = 0
х(1) = 3π/4 + 2kπ (k ∈ Z)
x(2) = 5π/4 + 2kπ (k ∈ Z)
1. Вынести за скобки общий множитель:
cos (x)(2cos (x) + √2) = 0
cos (x) = 0; 2cos (x) + √2 = 0.
2. Ищем x’ы:
cos (x) = 0
x = π/2 + kπ (k ∈ Z)
2cos (x) + √2 = 0
х(1) = 3π/4 + 2kπ (k ∈ Z)
x(2) = 5π/4 + 2kπ (k ∈ Z)
вы уверены что это правильно?
да. также можно заменить k в ответах на n (x(1) = n(1), x(2) = n(2)..)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад