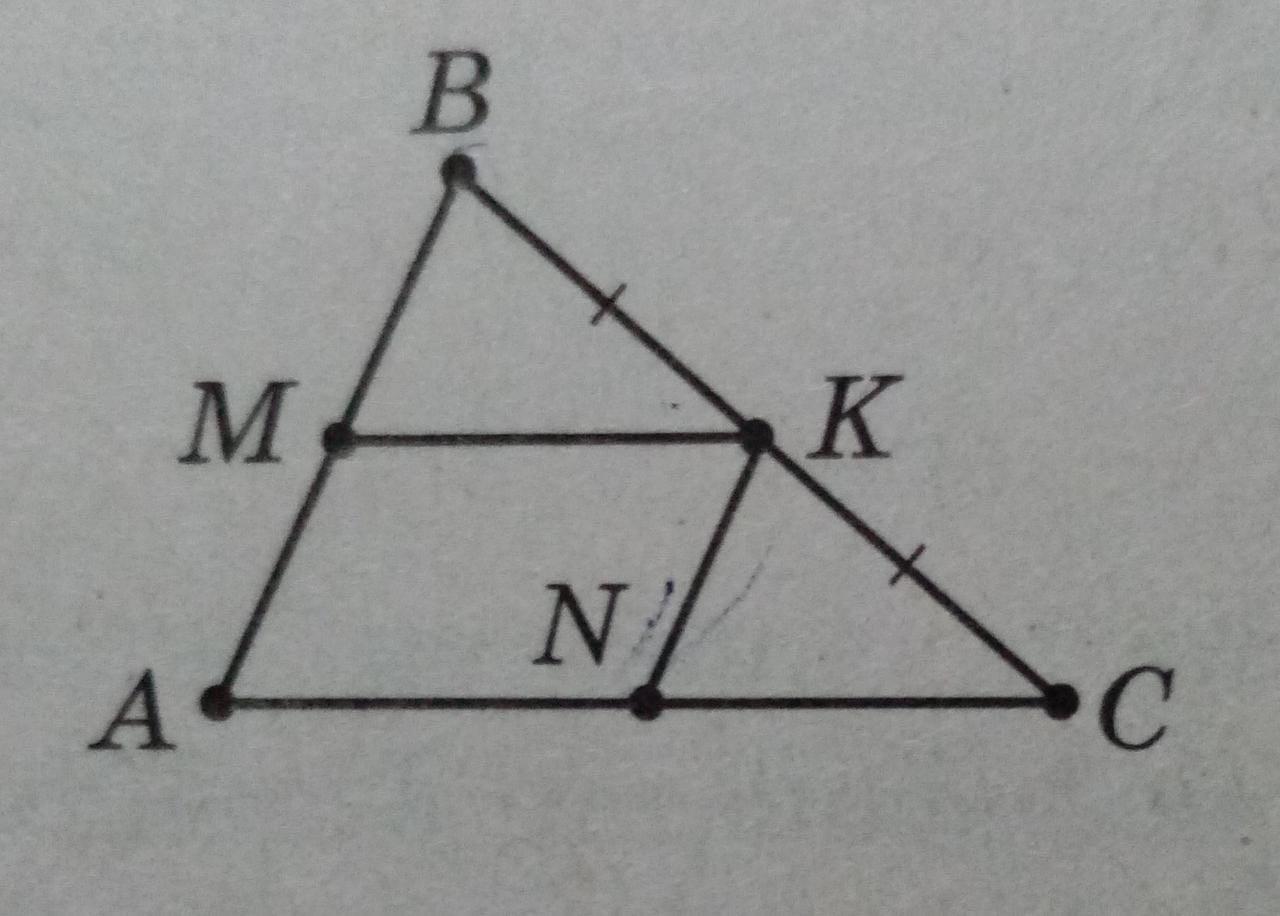
3. В треугольнике АВС (см. с. 36) сторона ВС равна 10. Через ее середину проведены двямые, параллельные сторонам АВ и АС. Периметр параллелограмма AMKN равен 12. Найдите периметр треугольника АВС.
Приложения:

Ответы
Ответ дал:
1
P(параллелограмма)=2*(NK+MK) , значит, NK+MK=12/2
NK+MK=6
Так как MK || AC и BK=KC
следовательно MK - средняя линия треугольника ABC
Аналогично, NK - средняя линия,
sloyrgg:
спасибо
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад