Ответы
Ответ дал:
2
Ответ:
Пошаговое объяснение:
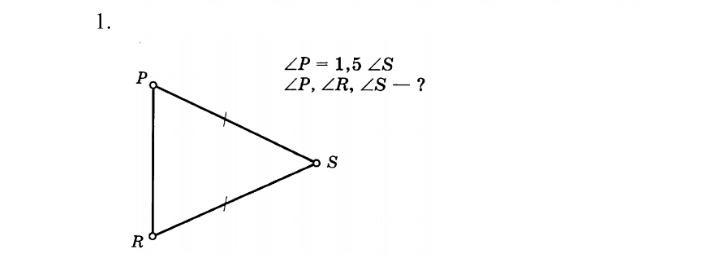
Так как PS=RS, то треугольник PSR с основанием PR боковыми сторонами PS и RS является равнобедренным.
Следовательно углы пр основании равны, то есть углы ∠SPR и ∠SRP равны. ==> ∠SPR = ∠SRP= 1,5*∠PSR
Сумма углов в треугольнике равна 180°. Тогда ∠SPR + ∠SRP + ∠PSR=180°
Подставляем в выражение известные нам значения:
(1,5*∠PSR)+(1,5*∠PSR)+∠PSR =180°
Упрощаем:
4 * ∠PSR= 180°
∠PSR = 45°
Находим углы при основании, то есть ∠SPR и ∠SRP, зная что оба угла равны 1,5*∠PSR
∠SPR = ∠SRP= 1,5 * 45°=67,5°
Делаем проверку, того что все углы в треугольнике в сумме дают 180°
67,5° + 67,5° + 45°=180°
Всё верно.
Ответ: ∠SPR = 67,5° , ∠SRP=67,5° , ∠PSR = 45°
seleznevaalisa255:
сотри последнюю строчку
2 последних
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад