Question

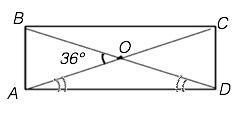
1)ABCD-прямоугольник.Угол BOA=36 ГРАДУСОВ.Найдите угол CAD и угол BDC
2)АВСD-прямоугольник. Угол ADB относится к углу СDB как 4:5. Найдите углы треугольника АОВ

Answer 1

Ответ:

1) ∆ АОD - равнобедренный, углы при его основании равны  

Для ∆ АОD угол АОВ по свойству внешнего угла треугольника равен сумме не смежных с ним углов: ∠ОАD +∠ODA=36°

∠САD=∠ODA=36°:2=18°

Угол АDC=90°, ⇒ ∠BDC=∠ADC-∠ODA=90°-18°=72°

2) Так как угол АDC - прямой то угол ADC=40°, а угол CDB=50°.

Так как диагонали прямоуголник равны и точкой пересечения делятся пополам, то треугольник АОВ равнобедренный, следовательно угол АВD=50° и угол ВАО=50°, тогда угол ВОА=180°-100°=80°

Пошаговое объяснение: