Question

ГЕОМЕТРИЯ 30 БАЛЛОВ, ОДНО ЗАДАНИЕ
Дан правильный тетраэдр SABC. Выполните рисунок. Найдите:

а) косинус угла между прямой SA и плоскостью ABC .

b) косинус угла между плоскостями SВC и ABC . Известно, что длина ребра 8 см.

Answer 1

Ответ:

$a) \frac{\sqrt{3} }{3}; ~~b) \frac{1}{3}$

Объяснение:

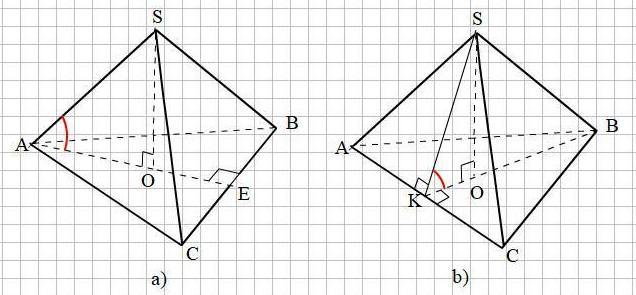
Смотри прикреплённый рисунок.

Пусть а = 8 см - ребро тетраэдра

a) В основании АВС проведём высоту АЕ ⊥ ВС.    АЕ = 0,5а√3;

Опустим высоту SO на плоскость АВС.

$AO=\frac{2}{3} AE = \frac{2}{3}\cdot a\frac{\sqrt{3} }{2} = \frac{a\sqrt{3} }{3}.$

Угол между прямой SA и плоскостью АВС есть угол SAO

b) В основании АВС проведём высоту BK ⊥ AС.    BK = 0,5а√3;

Опустим высоту SO на плоскость АВС.

$KO= \dfrac{1}{2} BK = \dfrac{1}{3}\cdot \dfrac{a\sqrt{3} }{2} =\dfrac{a\sqrt{3} }{6}$

Проведём в грани SAC апофему SK = 0,5а√3

Угол между плоскостями SAC и АВС есть угол SKO между апофемой SK и высотой основания ВК как угол между двумя перпендикулярами, восставленными из точки К к линии пересечения АС плоскостей  SAC и АВС

Поскольку тетраэдр правильный, то углы между  любой боковой плоскостью и плоскостью основания  равны между собой. И косинус между плоскостью SBC и плоскостью АВС равен 1/3.