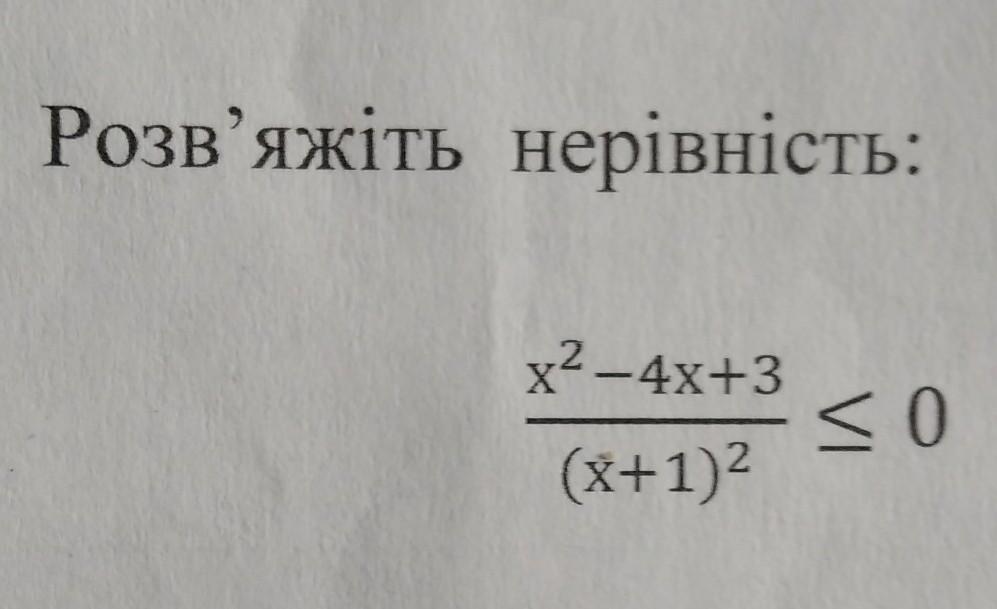Ответы
Ответ дал:
1
Ответ:
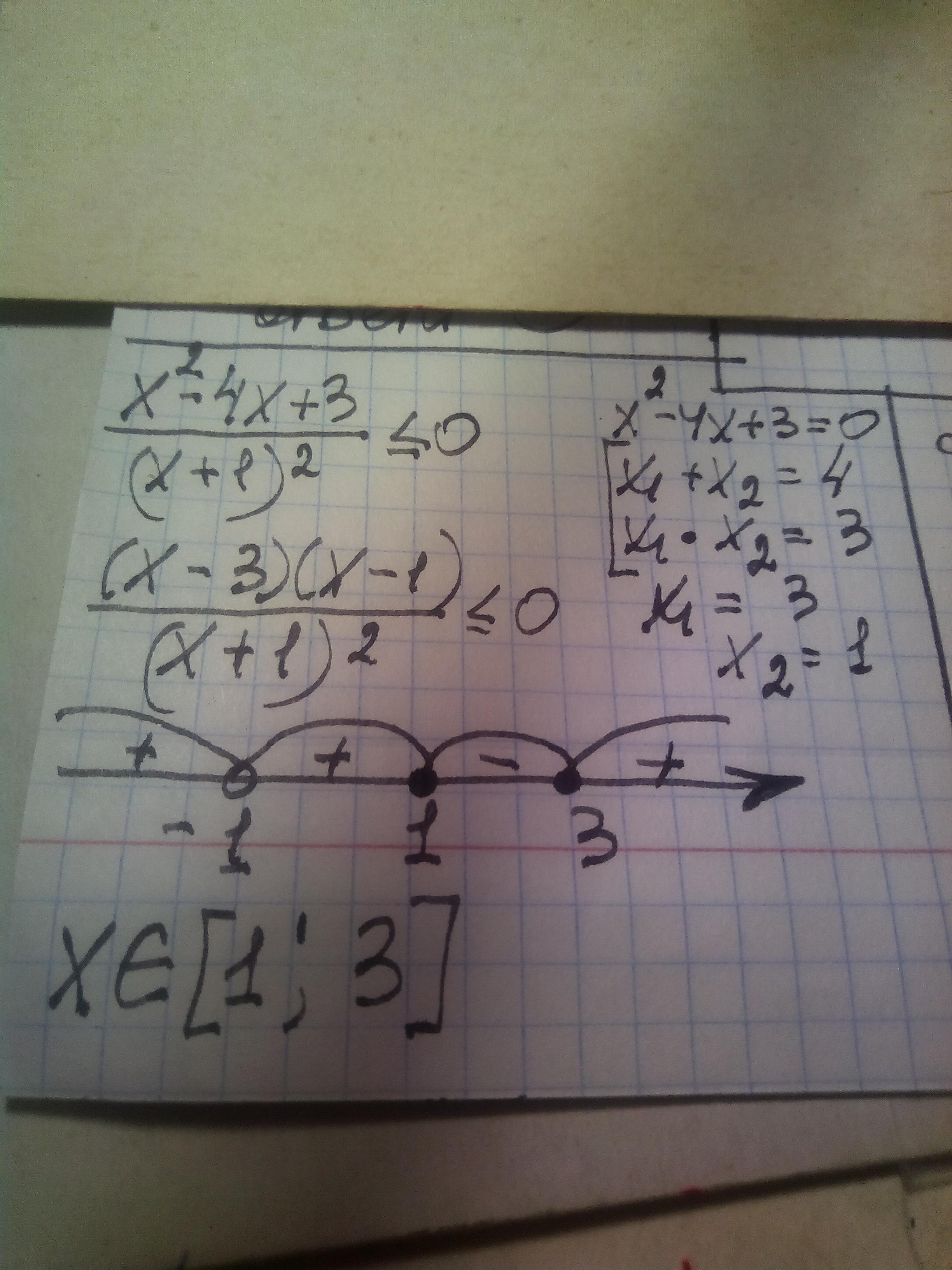
решение смотри на фотографии
Объяснение:
Приложения:
Ответ дал:
1
Ответ:
x= "квадратні дужки" 1, 3 "квадратні дужки"
Объяснение:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад