Question

Найдите площадь равнобедренной трапеции, описанной около окружности радиусом 5 см, если боковая сторона трапеции равна 12см

Answer 1

Ответ:

Объяснение:см. во вложении

Answer 2

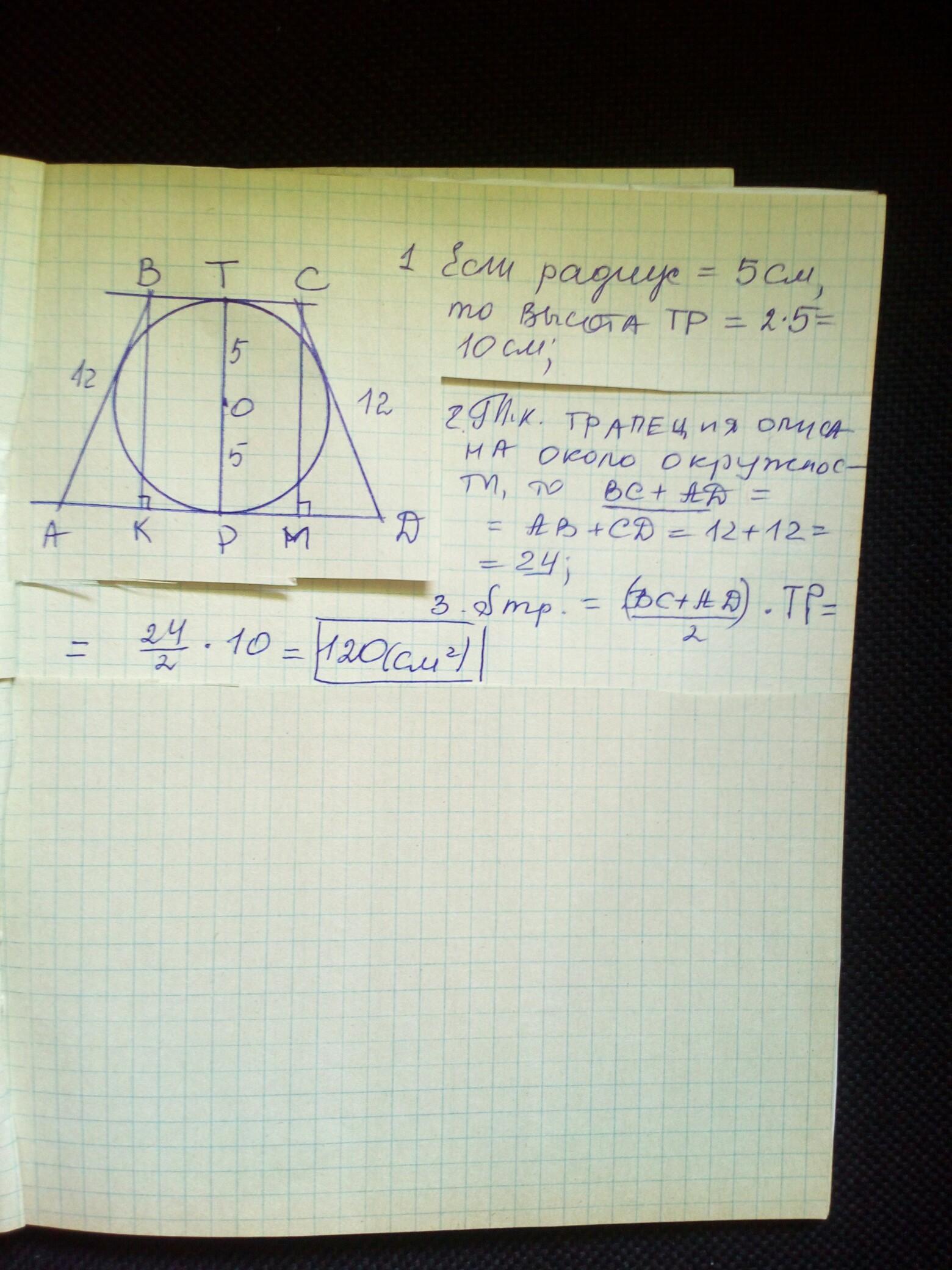
Ответ:   120 см² .

Объяснение:

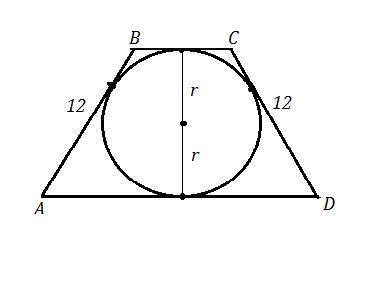
АВСД - равнобокая трапеция, АВ=СD-12 см ,  радиус вписан. окр. r=5 см .

Так как окружность вписана в четырёхугольник, то равны суммы противоположных сторон :  АВ+СD=BC+AD=12+12=24 cм .

Высота трапеции  h=2r=10 cм .

$S=\dfrac{a+b}{2}\cdot h=\dfrac{24}{2}\cdot 10=12\cdot 10=120$  см² .