Question

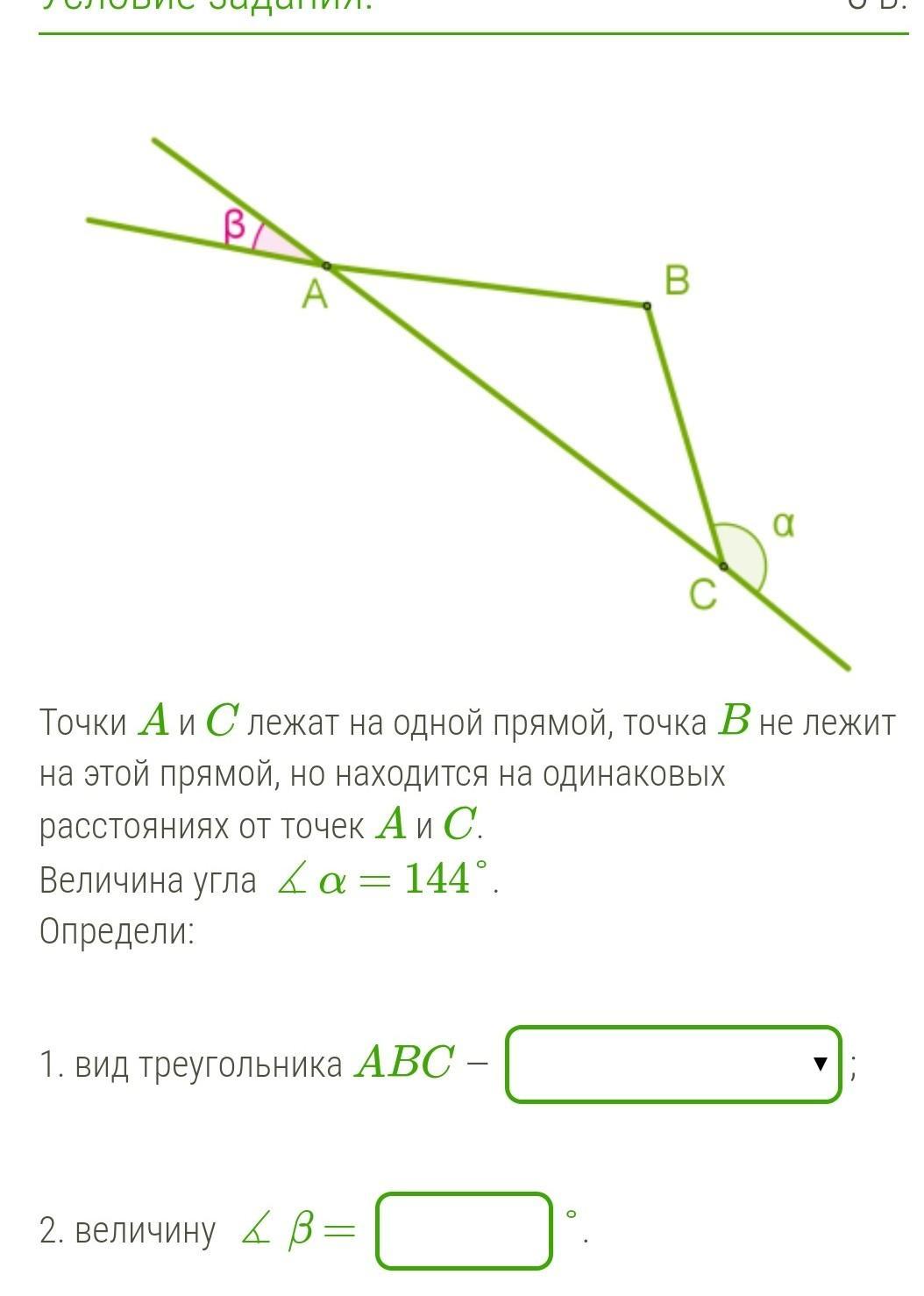
Точки A и C лежат на одной прямой, точка B не лежит на этой прямой, но находится на одинаковых расстояниях от точек A и C.

Величина угла ∡α = 144°.

Определи:

 

1. вид треугольника ABC — равностороннийравнобедренныйпрямоугольныйостроугольный;

 

2. величину ∡β = °.

​

Answer 1

Ответ:

Равнобедренный; 36°.

Пошаговое объяснение:

1. Так как AB = AC (из условия), ΔABC - равнобедренный.

2. ∠BCA смежный с α, поэтому их сумма равна 180°. Найдем ∠BCA:

∠BCA = 180° - α = 180° - 144° = 36°

Так как ΔABC равнобедренный (доказано в (1)), ∠BAC = ∠BCA как углы при основании.

β = ∠BAC как вертикальные углы (образованы пересечением прямых AB и AC). β = ∠BAC = ∠BCA = 36°.

Answer 2

Ответ:

Пошаговое объяснение:

Ответ:

Равнобедренный; 36°.

Пошаговое объяснение:

1. Так как AB = AC (из условия), ΔABC - равнобедренный.

2. ∠BCA смежный с α, поэтому их сумма равна 180°. Найдем ∠BCA:

∠BCA = 180° - α = 180° - 144° = 36°

Так как ΔABC равнобедренный (доказано в (1)), ∠BAC = ∠BCA как углы при основании.

β = ∠BAC как вертикальные углы (образованы пересечением прямых AB и AC). β = ∠BAC = ∠BCA = 36°.