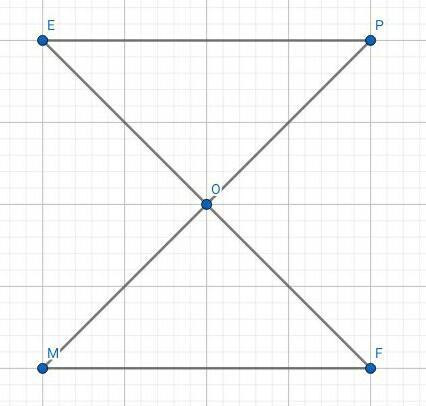
2) Отрезки EF и PM пересекаются в их
середине O. Докажите, что PE
параллельно MF.
Нужно с рисунком даю 35б
Ответы
Ответ дал:
1
Дано:
EF ∩ PM = O
O - середина ЕF и РМ.
Доказать:
РЕ || MF
Решение:
Рассмотрим △ЕОР и △MOF:
EO = OF, так как О - середина.
РО = ОМ, так как О - середина.
Вертикальные углы равны.
∠ЕОР = ∠MOF, как вертикальные.
=> △ЕОР = △MOF, по 1 признаку равенства треугольников.
Если накрест лежащие углы равны, то прямые параллельны.
Так △ЕОР = △MOF => ∠OEP = ∠OFM, ее накрест лежащие.
=> РЕ || MF
Ч.Т.Д.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад