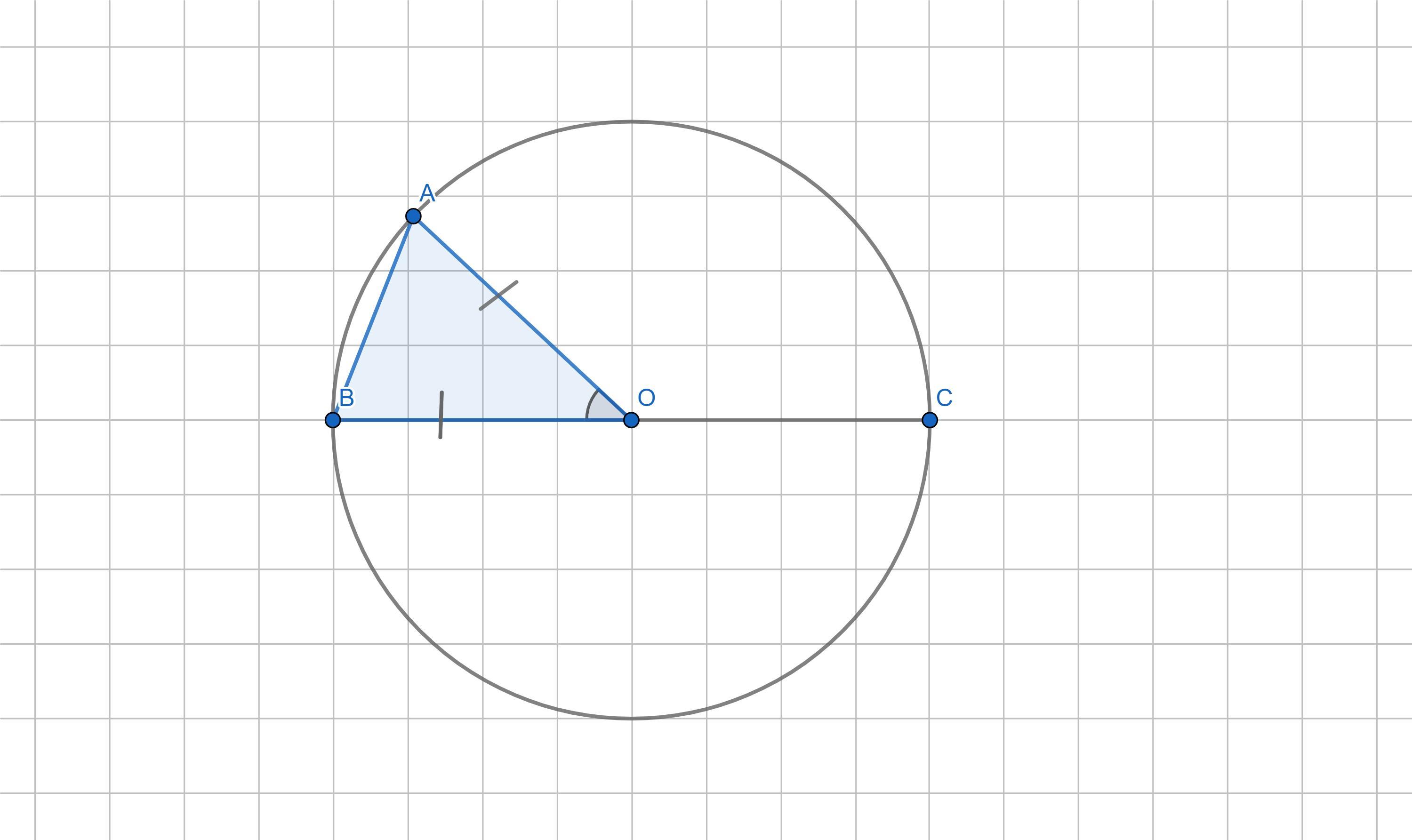
Точки A , B , C лежат на окружности с центром в точке O. Чему равен ⦟ABC, если известно, что BC является диаметром данной окружности, а ⦟AOB = 66°.
Помогите,пожалуйста.
Ответы
Ответ дал:
3
Решение:
Так как АО и ОВ - радиусы => АО = ОВ
=> △АВО - равнобедренный
Сумма углов треугольника равна 180°
180° - 66° = 114° - сумма ∠ВАО и ∠АВО
∠ВАО = ∠АВО (он же ∠АВС), по свойству равнобедренного треугольника.
=> ∠ВАО = ∠АВО (он же ∠АВС) = 114°/2 = 57°
Ответ: 57°
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад