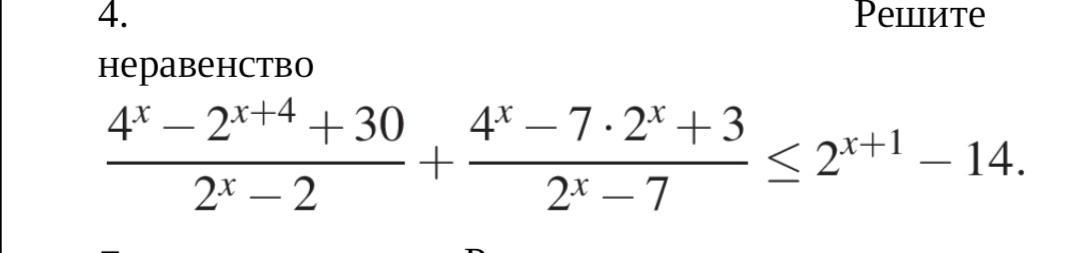Ответы
Ответ дал:
0
Покажу один из сопособов решения таких неравенств
1) проверим ограничения
2) введем замену
получаем,
А далее самое интересное
будем делить многочлен на многочлен
_t²-16t+30 | t-2 и _t²-7t+3 | t-7
t²-2t ______ t²-7t _____
_____ t-14 ____ t
_ -14t+30 3 (остаток)
-14t+28
------------
2 (остаток)
тогда
теперь все совсем просто
решаем методом интервалов
__-____ 2 ___+____4___-____7___+____
Не забываем проверить ограничение
Ответ (-∞; 1)∪[2; log₂7)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад