Question

Кут між бісектрисою та висотою прямокутного трикутника, які проведено з вершини прямого кута, дорівнює
10
o
. Знайдіть кути трикутника

Answer 1

Ответ: угол А=45°, угол В=35°

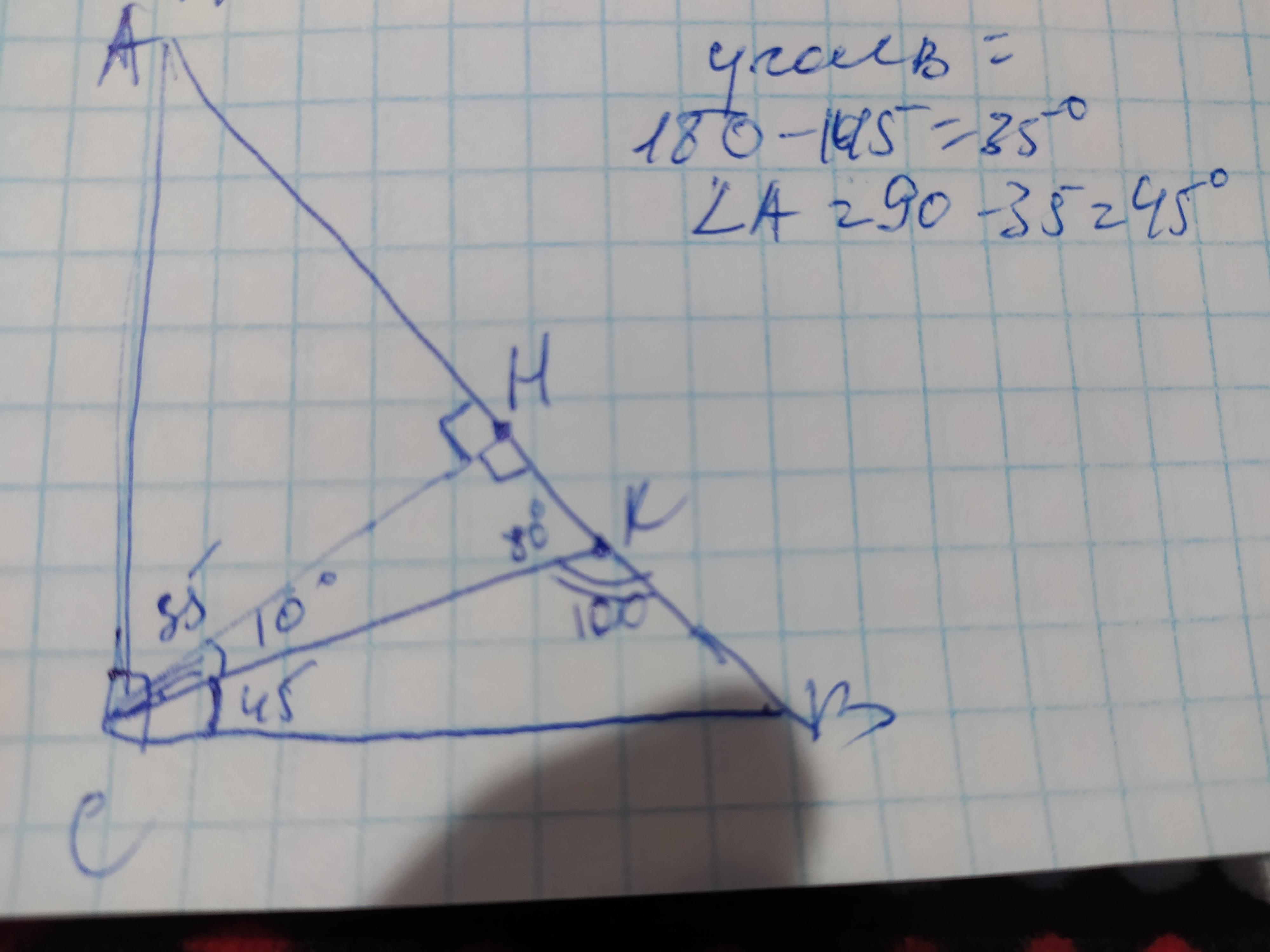
Объяснение: обозначим вершины треугольника А В С, где угол С=90°, высоту–СН, биссектрису СК. Так как биссектриса делит угол С пополам то угол КСВ=45°. Рассмотрим полученный ∆СНК. Он прямоугольный: угол СНК=90°; угол КСН=10°, так как сумма острых углов прямоугольного треугольника составляет 90°, то угол СКН=90-10=80°. Теперь рассмотрим полученный ∆КВС. Угол СКВсмежный с углом СКН и так как сумма смежных углов составляет 180°, то

угол СКВ=180-80=100°. Также в этом треугольнике мы нашли угол КСВ=45°. Так как сумма углов треугольника составляет 180°, то

угол В=180-100-45=35°. Теперь найдём угол А. Угол А=90-35°=45°