Question

СРОЧНО!!!
Геометрия
ДАЮ 38 балов.

28 номер

Answer 1

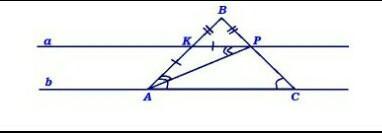
Дано:

△АВС

АВ = ВС

К ∈ АВ

Р ∈ ВС

АК = КР

∠РАС = 40°

∠BСА = 80°

Найти:

а || b?

Решение:

Так как АВ = ВС => △АВС - равнобедренный

∠BАС = ∠BСА = 80˚, по свойству равнобедренного треугольника.

Так как АК = КР => △АКР - равнобедренный

∠КРА = ∠КАР, по свойству равнобедренного треугольника

Итак, весь ∠BАС = 80°, а ∠РАС = 40° => ∠КАР = 80° - 40° = 40°

Так как ∠КРА = ∠КАР => КРА = 40°

Сумма углов треугольника равна 180°.

=> ∠АКР = 180° - (40° + 40°) = 100°

Если сумма односторонних углов равна 180°, то прямые параллельны.

∠АКР и ∠BАС - односторонние

Проверим, равняется ли их сумма 180°:

80° + 100° = 180°

=> а || b

Ответ: да, а || b.