Question

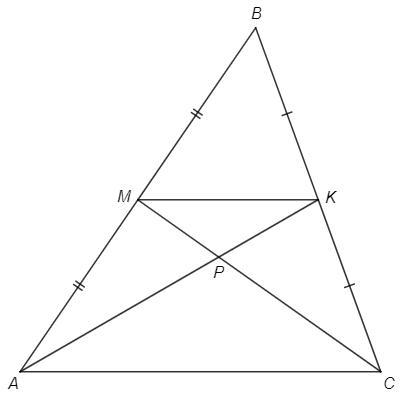
В треугольнике △ABC медианы AK и CM пересекаются в точке P. Докажите, что S△MBK=k⋅S△MKP, где k - натуральное число.
Найдите значение k.

Answer 1

Ответ:

k = 3

Объяснение:

Answer 2

Медианы треугольника делятся точкой пересечения в отношении 2:1 от вершины.

CP/PM =2/1 => CM/PM =3/1

Площади треугольников с равными высотами относятся как их основания.

S(MKC)/S(MKP) =CM/PM =3/1

BK=KC (K - середина BC)

S(MBK) =S(MKC) =3 S(MKP)

(3 - целое положительное, то есть натуральное число)