Сравните числа a и b.
Приложения:
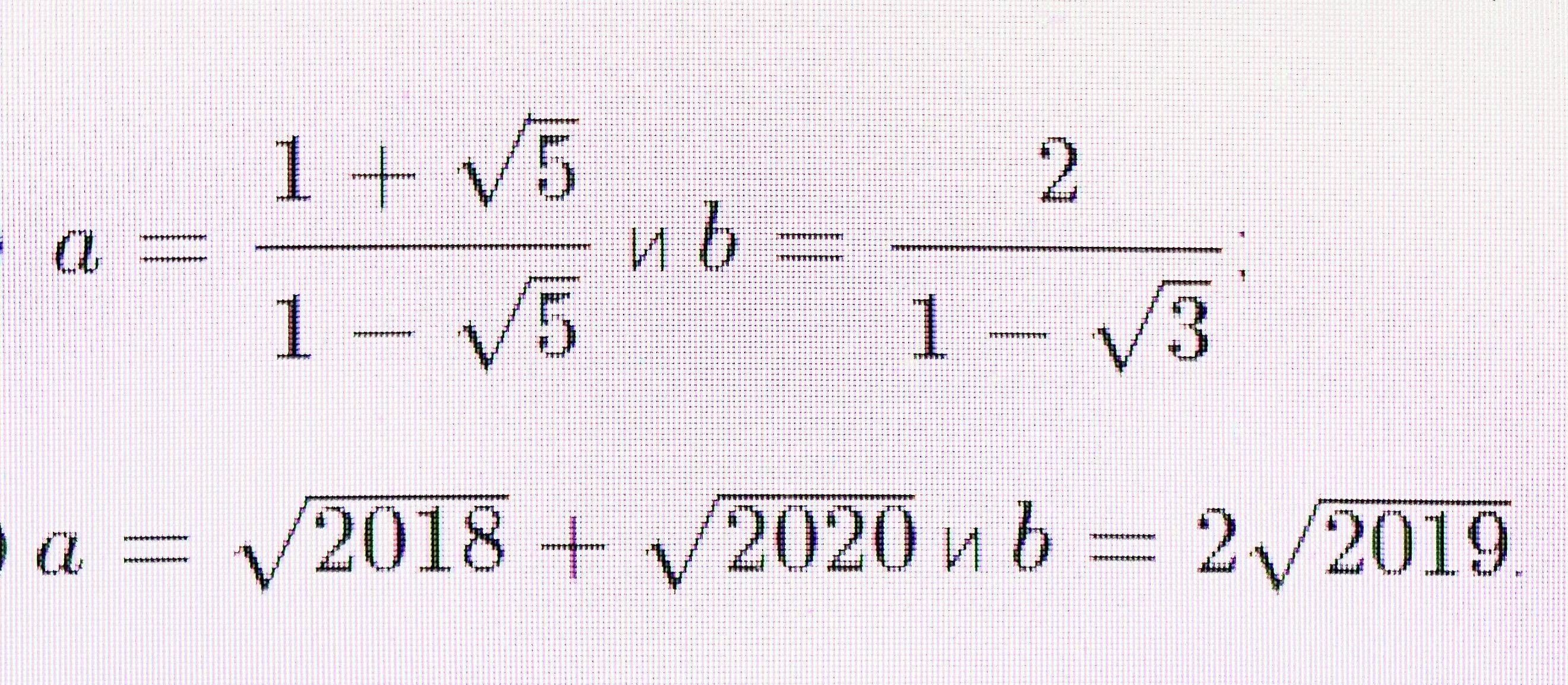
Simba2017:
второй заметный пример!
в нем а больше b
Почему?
ну если его расписывать, придется и первый
Можно хотя бы и просто 2
да ладно, оба распишу, ждите...
Благодарю
Ответы
Ответ дал:
1
1)избавлюсь от иррациональности в знаменателе, умножу числитель и знаменатель а на 1+√5, получу (1+√5)^2/(-4)=(6+2√5)/(-4)=-1.5-0.5√5
с b то же сделаю домножив все на 1+√3, получу
b=2(1+√3)/(-2)=-1-0.5√3
a-b=-1.5-0.5√5-(-1-0.5√3)=-0.5-0.5(√5-√3)<0, поэтому a<b
2) пусть 2019=x; 2018=x-1;2020=x+1
числа а и b положительны и больше 1. поэтому я сравню их квадраты, это равносильное сравнение
a^2=(√(x-1)+√(x+1))^2=x-1+x+1+2√((x-1)(x+1))=2x+2√((x-1)(x+1))=2x+2√(x^2-1)
b^2=4x
рассмотрим их разность
a^2-b^2=2√(x^2-1)-2x=2√(x^2-1)-2√(x^2)<0,
поэтому a^2<b^2 и a<b
В первом случае b=-1-√3, из-за этого дальше сложнее, но все равно спасибо
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад