Question

Две окружности 1 S и 2 S одинакового радиуса касаются в точке A . Третья окруж-
ность 3 S такого же радиуса проходит через точку A и вторично пересекает окружности 1 S и 2 S в точках B и C . Докажите, что BC – диаметр окружности 3 S

Answer 1

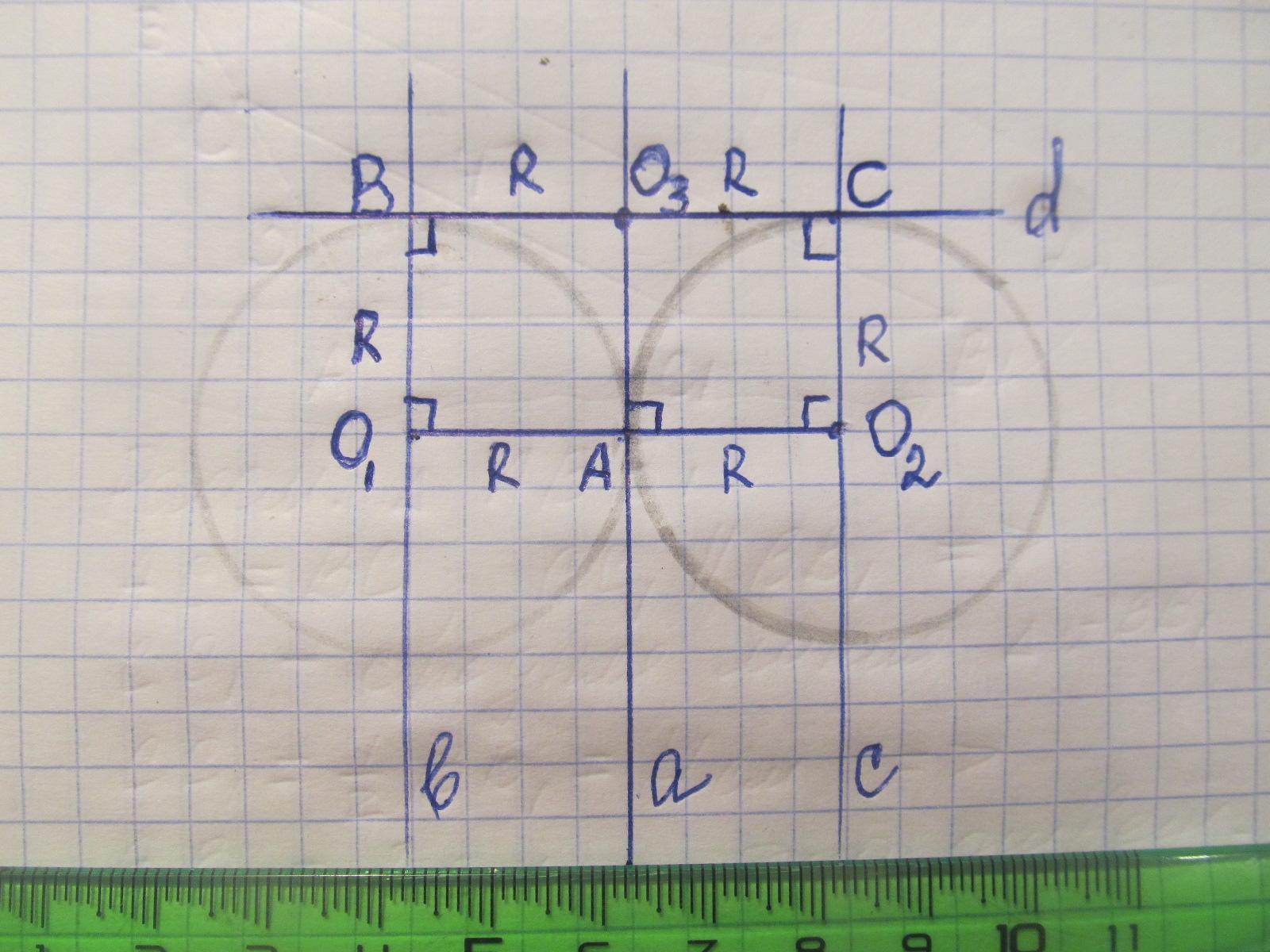
Начертим окружности равных радиусов, касающихся в т.А.

Касательная а ⊥ О1А и ⊥ О2А.

Проведем прямые в и с ║ а.

Прямые  в  и  с  ⊥  О1О2.   Точки В и С их точки пересечения с окружностями.  ВС - общая касательная для окружностей.

О1ВСО2 - прямоугольник. Его стороны О1В и О2С равны и параллельны и прямые а  в  с  ⊥  О1О2.

Прямая  а  делит прямоугольник на 2 квадрата. со сторонами = R.

Отсюда О3В=О3А=О3С=R.

А значит О3 - центр искомой окружности и ее диаметр = ВС.