Question

(25 БАЛЛОВ!!!) Медианы LP и MQ треугольника KLM перпендикулярны и пересекаются в точке G. Найдите PQ, если KL = 22 и KM = 31. ЖЕЛАТЕЛЬНО ПОДРОБНОЕ РЕШЕНИЕ​

Answer 1

1 способ:

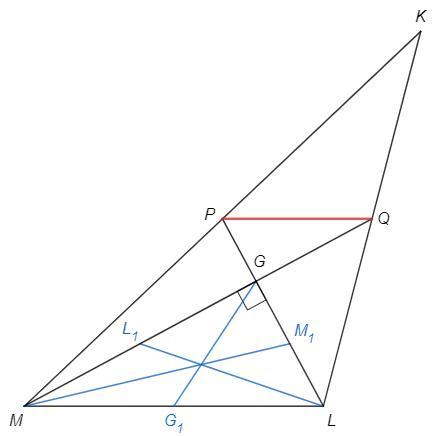
Медианы треугольника делятся точкой пересечения в отношении 2:1 от вершины.

MG=2x, GQ=x, LG=2y, GP=y

MP=KM/2, LQ=KL/2

Теорема Пифагора

4x^2 +y^2 =MP^2

x^2 +4y^2 =LQ^2

5x^2 +5y^2 =MP^2 +LQ^2

PQ =√(x^2 +y^2) =√((MP^2 +LQ^2)/5) =√((KM^2 +KL^2)/20) =8,5

2 способ:

Докажем свойство медиан прямоугольного треугольника

MM1, LL1, GG1 - медианы MLG

MM1^2 =MG^2 +LG^2/4

LL1^2 =MG^2/4 +LG^2

GG1^2 =ML^2/4

MM1^2 + LL1^2 =5/4 (MG^2+LG^2) =5/4 *ML^2 =5 GG^2

M1G=GP (LG:GP=2:1, LM1=M1G)

MG - медиана и высота => PMM1 - равнобедренный, MM1=MP=KM/2

Аналогично LL1=KL/2

GG1=ML/2 (медиана из прямого угла)

MM1^2 +LL1^2 =5 GG^2 (свойство медиан прямоугольного треугольника)

KM^2 +KL^2 =5 ML^2

ML =√((31^2 +22^2)/5) =17

PQ =ML/2 =8,5 (средняя линия)