Ответы
Ответ дал:
0
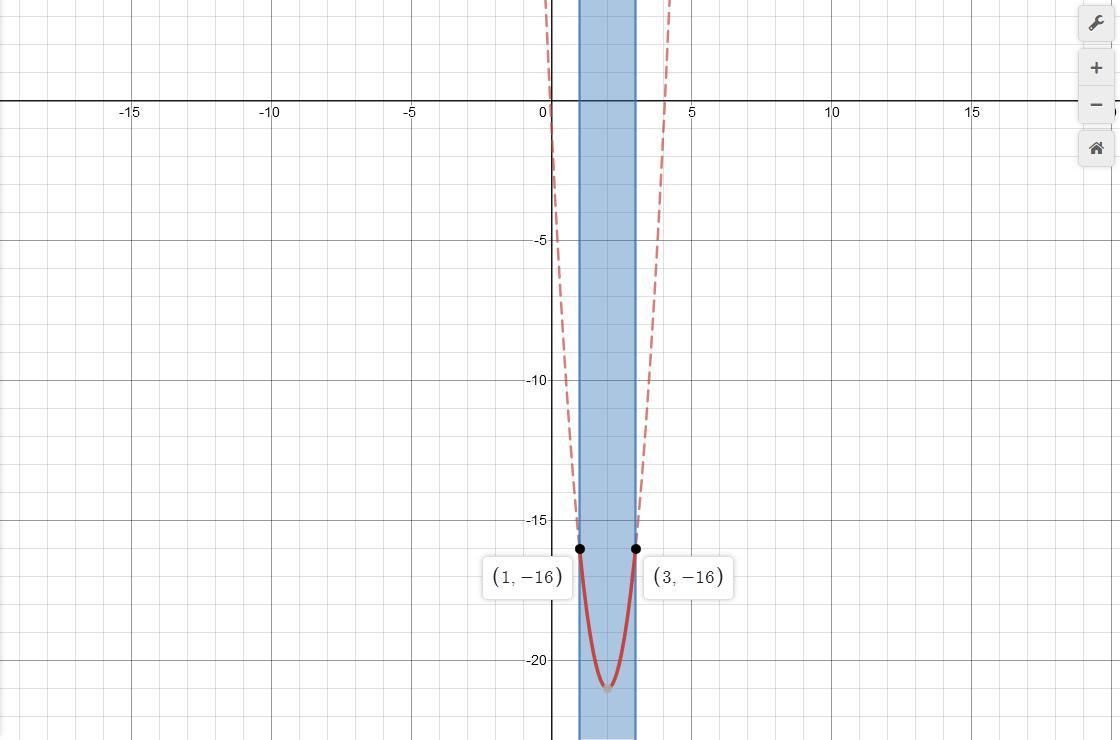
y = 5x^2-20x-1, x ∈ [1;3]
max y - ?
Решение:
y' = 10x-20
y' = 0
10x-20 = 0
10x = 20
x = 2 — критическая точка
- y(2) = 5·2^2-20·2-1 = 20-40-1 = -21
- y(1) = 5·1^2-20·1-1 = 5-20-1 = -16
- y(3) = 5·3^2-20·3-1 = 45-60-1 = -16
Ответ: max y(1) = -16 и max y(3) = -16; x ∈ [1;3].
Приложения:
Аноним:
максимум не эквивалентен наибольшему значению. поскольку точка максимума - точка, при переходе через которую производная меняет знак плюса на минус, а наибольшее не всегда является максимумом функции.
и не всякая критическая точка подозрительна на эту роль. надо бы подчеркнуть, что она входит в отрезок, поэтому вы проверяете значение функции в этой точке.
а впрочем. какая мне разница....
Вас заинтересует
1 год назад
2 года назад
7 лет назад