Ответы
Ответ дал:
3
Дано:
△АВС
АВ = 13 см
ВС = 20 см
АС = 21 см
Найти:
BD - ? (наименьшая высота)
Решение:
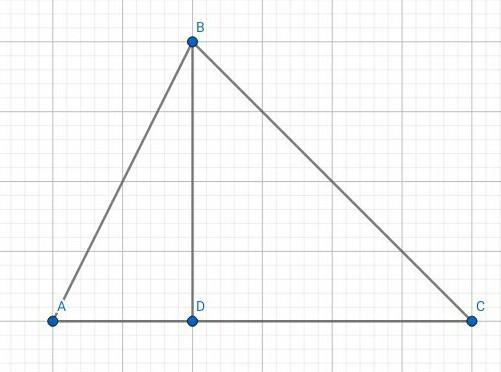
Наименьшая высота треугольника - высота, которая проведена из вершины В треугольника △АВС к основанию.
Проведём высоту BD к основанию.
Найдём площадь этого треугольника по теореме Герона:
S = √p(p - a)(p - b)(p - c)
p - полупериметр сторон а, b, c.
p = (a + b + c)/2 = (13 + 20 + 21)/2 = 54/2 = 27 см
S = √(27(27 - 13)(27 - 20)(27 - 21)) = √(27 * 14 * 7 * 6) = √15876 = 126 см²
Площадь треугольника находится ещё и таким образом:
S = 1/2основание * h
126 = 1/2 * 21 * h
h = 126 * 2/21 = 12 см
Ответ: 12 см.
Приложения:
dasha5d5d5d:
Спасибо большое ❤️
Здравствуйте, не за что, обращайтесь, если что-то будет непонятно. Всего доброго и до свидания!
формулу Герона пишут так: √{p(p-a)(p-b)(p-c)} , или так: √(p(p-a)(p-b)(p-c)) , или так: [tex] \sqrt{p(p-a)(p-b)(p-c)} [tex] у Вас как будто под корнем только p )))
Да, извините! ))) В решении написала, а в формуле нет))) Попрошу отправить на исправление чуть позже!)))
думаю, из за такого не стоит беспокоить модераторов
Я написала в вашем последнем ответе по геометрии замечание.
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад
