Предмет: Геометрия
Автор: binamaksimchuk
Вопрос задан 2 года назад

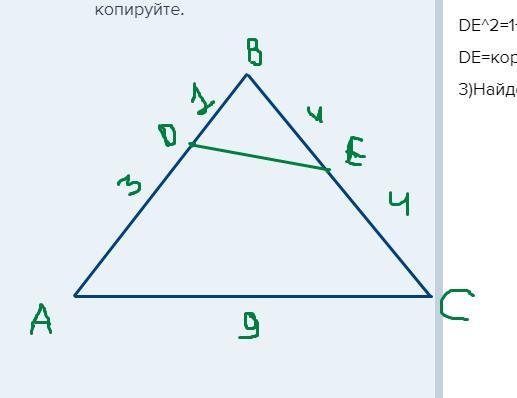
Дан треугольник ABC, на сторонах AB и BC которого отметили точки D и E соответственно. Известно, что EC=AB=4 см, AD=3 см, BC=8 см, AC=9 см. Найти DE,cosC
cos C я нашла (0,9),помогите найти DE.
Интересует решение именно ЭТОЙ задачи,аналоги из интернета не копируйте.

ужнеужели: Вы нашли косинус С по теореме косинусов. Так примените это к треугольнику АВС с углом В и найдите косинус угла В. Этот угол тупой и косинус будет равен - 1/64. А потом примените ту же теорему для Треугольника ДВЕ, зная косинус В и найдите ДЕ = корень из 137/8

Andr1806: Все это и было проделано пользователем prrpklass-1000090. Просто решение по моей вине было удалено, вместо отправки на доработку. (Удаленное содержание
Рассмотрим треугольник ABC, найдем косинус угла bcosB=16+64-81/2*4*8=-1/64рассмотрим треугольник DBEнайдем DEDE^2=1+16-2*4*cosBDE^2=1+16-2*4*-1/64=17+1/8=137/8DE=корень(137/8). В решении как раз не был найден косинус С. Конечно, мелочь. Извинения пользователю принесены.

binamaksimchuk: спасибо,я вчера всё сделала,благодаря идее prrpklass-1000090.

Tanda80: А, мне интересно: Вы написали, что значение ДЕ - целое число. Это, действительно, так? Если, да, то где же ошибка в рассуждениях Пррпкласс? У меня, например, тоже получилось, что ДЕ=корень из 137/8

binamaksimchuk: Я не переписала ответы,но по аналогии с ответом по косинусу С ,которое комп засчитал мне как правильный(а я его округляла),скорее всего и длину DE просили округлить до целых.Это и сбило меня с толку