Question

Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции​

Answer 1

Дано:

Равнобедренная трапеция $ABCD$.

$BC = 7$.

$AD = 13$.

${S}_{TP.} = 40$

Найти:

$AB = CD = ?$

Решение:

Т.к. трапеция равнобедренная, то по свойству $AB=CD$.

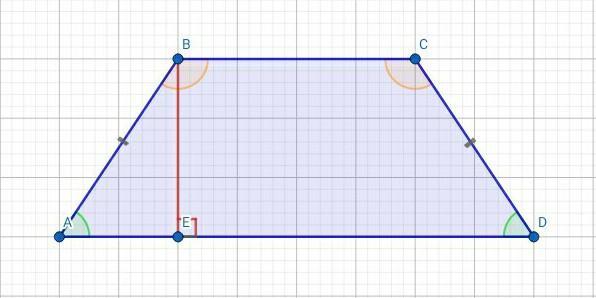
Проведём из вершины $B$ к основанию $AD$ равнобедренной трапеции $ABCD$ высоту $BE$. Найдём величину этой высоты.

Т.к. ${S}_{TP.}=\dfrac{AD+BC}{2} \cdot BE$, то $BE=\dfrac{2\cdot S}{AD+BC}=\dfrac{2\cdot 40}{13+7} = \dfrac{80}{20}=4$.

Когда мы опустили высоту $BE$, у нас образовался прямоугольный $\triangle BEA$, где $BE$ и $AE$ - катеты, $AB$ - гипотенуза.

По т.Пифагора $AB=\sqrt{AE^2+BE^2}$ ⇒ $AE=\dfrac{AD-BC}{2}=\dfrac{13-7}{2}=3$

$BE=4$, $AE=3$ ⇒$AB=\sqrt{4^2+3^2}=\sqrt{16+9}=\sqrt{25}=5$.

Ответ: $AB=CD=5$.